
Bernard's Watch
Fire! Fire!
| S 7 | Ep 13 | 2005/03/31 |
| TV Series Episode | - min | |
| COM | ||

The Berry Paradox
The phrase "the first number not nameable in under ten words" appears to name it in nine words.
| S - | Ep - | |
| High | - min | |
Consider the expression: "The smallest positive integer not definable in under eleven words." Since there are finitely many words, there are finitely many phrases of under eleven words, and hence finitely many positive integers that are defined by phrases of under eleven words. Since there are infinitely many positive integers, this means that there are positive integers that cannot be defined by phrases of under eleven words. If there are positive integers that satisfy a given property, then there is a smallest positive integer that satisfies that property; therefore, there is a smallest positive integer satisfying the property "not definable in under eleven words". This is the integer to which the above expression refers. The above expression is only ten words long, so this integer is defined by an expression that is under eleven words long; it is definable in under eleven words, and is not the smallest positive integer not definable in under eleven words, and is not defined by this expression. This is a paradox: there must be an integer defined by this expression, but since the expression is self-contradictory (any integer it defines is definable in under eleven words), there cannot be any integer defined by it.
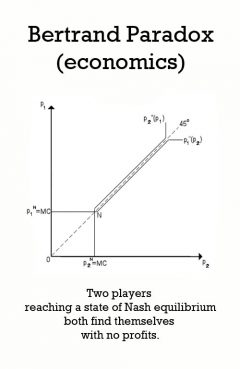
Bertrand Paradox (economics)
Two players reaching a state of Nash equilibrium both find themselves with no profits.
| S - | Ep - | |
| - min | ||
In economics and commerce, the Bertrand paradoxnamed after its creator, Joseph Bertrand describes a situation in which two players (firms) reach a state of Nash equilibrium where both firms charge a price equal to marginal cost. The paradox is that in models such as Cournot competition, an increase in the number of firms is associated with a convergence of prices to marginal costs. In these alternative models of oligopoly a small number of firms earn positive profits by charging prices above cost. Suppose two firms, A and B, sell a homogeneous commodity, each with the same cost of production and distribution, so that customers choose the product solely on the basis of price. It follows that demand is infinitely price-elastic. Neither A nor B will set a higher price than the other because doing so would yield the entire market to their rival. If they set the same price, the companies will share both the market and profits. On the other hand, if either firm were to lower its price, even a little, it would gain the whole market and substantially larger profits. Since both A and B know this, they will each try to undercut their competitor until the product is selling at zero economic profit. This is the pure-strategy Nash equilibrium. Recent work has shown that there may be an additional mixed-strategy Nash equilibrium with positive economic profits. The Bertrand paradox rarely appears in practice because real products are almost always differentiated in some way other than price (brand name, if nothing else); firms have limitations on their capacity to manufacture and distribute; and two firms rarely have identical costs. Bertrand's result is paradoxical because if the number of firms goes from one to two, the price decreases from the monopoly price to the competitive price and stays at the same level as the number of firms increases further. This is not very realistic, as in reality, markets featuring a small number of firms with market power typically charge a price in excess of marginal cost. The empirical analysis shows that in most industries with two competitors, positive profits are made. Solutions to the Paradox attempt to derive solutions that are more in line with solutions from the Cournot model of competition, where two firms in a market earn positive profits that lie somewhere between the perfectly competitive and monopoly levels.
Bertrand Paradox (probability)
Different common-sense definitions of randomness give quite different results.
| S - | Ep - | |
| High | - min | |
The Bertrand paradox is a problem within the classical interpretation of probability theory. Joseph Bertrand introduced it in his work Calcul des probabilit s (1889) as an example to show that probabilities may not be well defined if the mechanism or method that produces the random variable is not clearly defined. Bertrand's box paradox is a classic paradox of elementary probability theory. It was first posed by Joseph Bertrand in his Calcul des probabilit_s, published in 1889. There are three boxes: a box containing two gold coins, a box with two silver coins, and a box with one of each. After choosing a box at random and withdrawing one coin at random, if that happens to be a gold coin, it may seem that the probability that the remaining coin is gold is 1 2; in fact, the probability is actually 2 3. Two problems that are very similar are the Monty Hall problem and the Three Prisoners problem. These simple but slightly counterintuitive puzzles are used as a standard example in teaching probability theory. Their solution illustrates some basic principles, including the Kolmogorov axioms. --------------- The paradox as stated by Bertrand[edit source | editbeta] It can be easier to understand the correct answer if you consider the paradox as Bertrand originally described it. After a box has been chosen, but before a drawer is opened to let you observe a coin, the probability is 2/3 that the box has two of the same kind of coin. If the probability of "observing a gold coin" in combination with "the box has two of the same kind of coin" is 1/2, then the probability of "observing a silver coin" in combination with "the box has two of the same kind of coin" must also be 1/2. And if the probability that the box has two like coins changes to 1/2 no matter what kind of coin is shown, the probability would have to be 1/2 even if you hadn't observed a coin this way. Since we know his probability is 2/3, not 1/2, we have an apparent paradox. It can be resolved only by recognizing how the combination of "observing a gold coin" with each possible box can only affect the probability that the box was GS or SS, but not GG.

Bertud ng putik
| 2003/06/11 | ||
| Film | 105 min | |
| ACT ADV DRA | Phillippines | |
The year is 1953 and Gabriel de Dios, a man who lives a simple and happy life with his family, possesses the good half of a powerful amulet while Damian Buenavista, a black-hearted scoundrel, who intends to rule the world, owns the bad half. But Damian's plan to take control of the world will not be successful without the other half from Gabriel. Damian's plans, however, turn futile when Gabriels bertud, as the amulet is called, saves Gabriel and brings him to the year 2003. Gabriel thinks he is already safe from the greedy Damian... until he realizes the battle has just begun.
Bessatsu Olympia Kyklos
| S - | Ep - | 2020/04/ |
| TV Series | - min | |
| COM | Japan | |
The Thermae Romae manga author Mari Yamazaki's latest time-slip comedy Olympia Kyklos will be adapted into a TV anime series. It will be aired as a five-minute short series from April 2020 under the title Bessatsu Olympia Kykulos, and its characters will be animated with clay.

Best Friends Whenever
| S - | Ep - | 2015/06/26 |
| TV Series | 20 min | |
| COM FAM SF | ||
Follows teenagers Shelby (Taylor) and Cyd (Bender), who when a science experiment goes wrong, become unstuck in time leaping forward and backward in time. Teenage genius Barry then helps girls master their new power.

Best Friends Whenever
A Time To Travel
| S 1 | Ep 1 | 2015/06/26 |
| TV Series Episode | 23 min | |
| COM FAM SF | ||
Follows teenagers Shelby and Cyd. When a science experiment goes wrong, they become unstuck in time leaping forward and backward in time. Teenage genius Barry then helps the girls master their new power.

Best Friends Whenever
A Time To Cheat
| S 1 | Ep 2 | 2015/07/12 |
| TV Series Episode | 23 min | |
| COM FAM SF | ||
Cyd and Shelby have trouble studying and try to jump ahead in time to steal the test questions.

Best Friends Whenever
A Time To Say Thank You
| S 1 | Ep 3 | 2015/07/19 |
| TV Series Episode | 23 min | |
| COM FAM SF | ||
When Cyd tries to plan a special thank you for the Marcus family, Shelby steps in to help with hulu dancers, a rock band and jugglers and everything somehow leads to a big misunderstanding and a huge kitchen disaster.

Best Friends Whenever
A Time To Jump and Jam
| S 1 | Ep 4 | 2015/07/26 |
| TV Series Episode | 23 min | |
| COM FAM SF | ||
Cyd and Shelby revisit their favorite memory from middle school but their memories are skewed.

Best Friends Whenever
A Time To Rob and Slam
| S 1 | Ep 5 | 2015/08/09 |
| TV Series Episode | 23 min | |
| COM FAM SF | ||
When Shelby's new lab partner, The Rob, can't stop being mean and annoying, the girls travel back in time to try and find out why he's such a jerk.

Best Friends Whenever
The Butterscotch Effect
| S 1 | Ep 6 | 2015/08/16 |
| TV Series Episode | 23 min | |
| COM FAM SF | ||
Cyd and Shelby go back to change the past so that Barry can meet his childhood science hero. However, when they return, they realize Barry and Naldo have changed as well and are now terrible rock musicians instead of aspiring scientists.

Best Friends Whenever
A Time To Boogie (Shake Your Booty)
| S 1 | Ep 7 | 2015/08/23 |
| TV Series Episode | 23 min | |
| COM FAM SF | ||
When the girls are assigned to do a report on the 1970s disco era, they decide to travel back and experience the 70s firsthand and land in the midst of a turf battle between the disco and punk kids.

Best Friends Whenever
Jump To The Future Lab (Back To The Future Lab)
| S 1 | Ep 8 | 2015/09/20 |
| TV Series Episode | 23 min | |
| COM FAM SF | ||
Cyd and Shelby discover a major clue to the future lab memory and it is somehow tied to Barry's science idol Janet Smythe, who also employs Shelby's dad.

Best Friends Whenever
Cyd and Shelby's Haunted Escape
| S 1 | Ep 9 | 2015/10/04 |
| TV Series Episode | 23 min | |
| COM FAM SF | ||
Cyd and Shelby use Barry's new invention to teleport themselves to New York City's Spooktacular in Central Park and get trapped in a haunted house with Riley and Lucas from "Girl Meets World."

Best Friends Whenever
When Shelby Met Cyd
| S 1 | Ep 10 | 2015/10/25 |
| TV Series Episode | 23 min | |
| COM FAM SF | ||
When Cyd and Shelby go back to kindergarten to celebrate their friendship anniversary and relive the day they first met, they begin to change back to their five-year-old selves.

Best Friends Whenever
Cyd and Shelby Strike Back, Part 1
| S 1 | Ep 11 | 2015/11/27 |
| TV Series Episode | 45 min | |
| COM FAM SF | ||
The girls travel back in time to stop Janet Smythe from starting GDD; their plan works but they also manages to stop major events from happening. - Part 1

Best Friends Whenever
Cyd and Shelby Strike Back, Part 2
| S 1 | Ep 12 | 2015/11/27 |
| TV Series Episode | 45 min | |
| COM FAM SF | ||
The girls travel back in time to stop Janet Smythe from starting GDD; their plan works but they also manages to stop major events from happening. - Part 2

Best Friends Whenever
The Girls of Christmas Past
| S 1 | Ep 13 | 2015/12/06 |
| TV Series Episode | 23 min | |
| COM FAM SF | ||
Cyd travels back to Christmas the year before to try and figure out the perfect gift for Shelby. Meanwhile, Barry and Naldo's Winter Wonderland experiment sparks an elf war, with Bret and Chet leading the charge.