
Devs
8 Episodes
| S - | Ep - | 2020/03/05 |
| TV Miniseries | 379 min TV-MA | |
| DRA MYS SF | USA | |
A computer engineer investigates the secretive development division in her company, which she believes is behind the disappearance of her boyfriend.

Devs
Episode # 1.1
| S 1 | Ep 1 | 2020/03/05 |
| TV Miniseries | 55 min TV-MA | |
| DRA MYS SF | USA | |
When her boyfriend Sergei vanishes after starting a new job at the secretive Devs division of tech company Amaya, software engineer Lily begins to suspect that his disappearance may not be as clear-cut as it seems.

Devs
Episode # 1.2
| S 1 | Ep 2 | 2020/03/05 |
| TV Miniseries | 50 min TV-MA | |
| DRA MYS SF | USA | |
Lily enlists ex-boyfriend Jamie's help to investigate Sergei's disappearance. She begins to question what she really knew about Sergei.

Devs
Episode # 1.3
| S 1 | Ep 3 | 2020/03/12 |
| TV Miniseries | 1 min TV-MA | |
| DRA MYS SF | USA | |
Lily returns to work at Amaya and explains her suspicions to Jen and Anya. Forest is visited by Laine, a powerful senator asking questions about the Devs project.

Devs
Episode # 1.4
| S 1 | Ep 4 | 2020/03/19 |
| TV Miniseries | 1 min TV-MA | |
| DRA MYS SF | USA | |
After Lily's behavior at Amaya, Kenton forces her to see a psychiatrist. Meanwhile, the Devs team disagree over the ethics of their invention, and Forest asserts his commitment to the project.

Devs
Episode # 1.5
| S 1 | Ep 5 | 2020/03/26 |
| TV Miniseries | 1 min TV-MA | |
| DRA MYS SF | USA | |
Kenton pays Jamie a visit to guarantee his silence, while Katie covertly exploits the Devs system for her own ends.

Devs
Episode # 1.6
| S 1 | Ep 6 | 2020/04/02 |
| TV Miniseries | 1 min TV-MA | |
| DRA MYS SF | USA | |
Lily and Jamie visit Forest looking for answers, and Katie reveals to Lily the true nature of the Devs system.

Devs
Episode # 1.7
| S 1 | Ep 7 | 2020/04/09 |
| TV Miniseries | 1 min TV-MA | |
| DRA MYS SF | USA | |
The Devs team perfect the system, and Forest and Katie wait for the completion of the Devs project. Lily and Jamie try to avoid its threat, but a visit from Kenton leaves Lily with no choice.

Devs
Episode # 1.8
| S 1 | Ep 8 | 2020/03/12 |
| TV Miniseries | 1 min TV-MA | |
| DRA MYS SF | USA | |
The question is answered: is the Universe deterministic, a multi-verse, or something else?

Dexter's Laboratory
Dee Deemensional
| S 1 | Ep 1 | 1996/04/28 |
| TV Series Episode | 8 min | |
| COM DRA | ||
Dee Dee time-travels to save Dexter from a monster.

Dexter's Laboratory
Morning Stretch
| S 2 | Ep 4 | 1997/08/06 |
| TV Series Episode | - min TV-G | |
| COM DRA | ||
Dexter invents a helmet that stretches 30 seconds into 30 minutes... but only for him.

Dexter's Laboratory
Backfire
| S 2 | Ep 5 | 1997/08/13 |
| TV Series Episode | 30 min TV-G | |
| COM DRA | ||
Dexter tries to improve the family car's ability to travel through time, but Dee Dee throws a wrench into his plan.

Dexter's Laboratory
Old Flame
| S 2 | Ep 28 | 1998/02/28 |
| TV Series Episode | 8 min TV-G | |
| COM DRA | ||
Dexter wants to meet the original genius who invented fire and zips back in time. He grabs the unsuspecting and frightened caveman and brings him back to the lab.

Dexter's Laboratory
sdrawckaB
| S 2 | Ep 33 | 1998/04/01 |
| TV Series Episode | - min | |
| COM DRA | ||
Dexter develops a reverse belt. While wearing the belt to get a snack in the kitchen, Dee Dee sneaks into the lab to play with the belt controls.

Dexter's Laboratory Ego Trip
| S - | Ep - | 1999/12/31 |
| TV Movie | 50 min | |
After Dexter is confronted with robots who wish to "destroy the one who saved the future," he uses his time machine to see how he saved it. After receiving a message from the future, Dexter travels through time and meets four different versions of himself.

"Diamond Doubles"
| S - | Ep - | 2013/07/16 |
| Short Story | - min | |
A novel writer from the fourth millennium is trapped in the 1960s and subjecting a contemporary editor to his work.
Diamond-Water Paradox (Paradox Of Value)
Water is more useful than diamonds, yet is a lot cheaper.
| S - | Ep - | |
| - min | ||
The paradox of value (also known as the diamond_water paradox) is the apparent contradiction that, although water is on the whole more useful, in terms of survival, than diamonds, diamonds command a higher price in the market. The philosopher Adam Smith is often considered to be the classic presenter of this paradox, although it had already appeared as early as Plato's Euthydemus. Nicolaus Copernicus, John Locke, John Law and others had previously tried to explain the disparity.
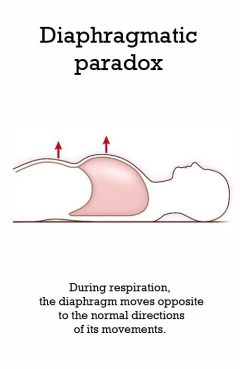
Diaphragmatic Paradox
During respiration, the diaphragm moves opposite to the normal directions of its movements.
| S - | Ep - | |
| - min | ||
Diaphragmatic paradox or paradoxical diaphragm phenomenon is an abnormal medical sign observed during respiration, in which the diaphragm moves opposite to the normal directions of its movements. The diaphragm normally moves downwards during inspiration and upwards during expiration. But in diaphragmatic paradox, it moves upwards during inspiration and downwards during expiration.

Diary of Tristram Shandy
To document each day of your life, only by living forever could no moment remain unwritten.
| S - | Ep - | |
| - min | ||
The diary of Tristram Shandy[edit source | editbeta] Tristram Shandy, the hero of a novel by Laurence Sterne, writes his autobiography so conscientiously that it takes him one year to lay down the events of one day. If he is mortal he can never terminate; but if he lived forever then no part of his diary would remain unwritten, for to each day of his life a year devoted to that day's description would correspond.
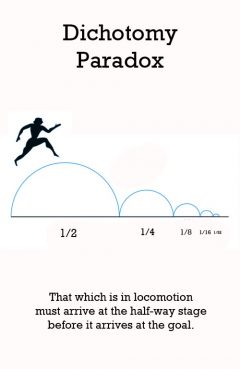
Dichotomy Paradox
That which is in locomotion must arrive at the half-way stage before it arrives at the goal.
| S - | Ep - | -460// |
| High | - min | |
That which is in locomotion must arrive at the half-way stage before it arrives at the goal._ as recounted by Aristotle, Physics VI:9, 239b10 ii. The Dichotomy (The Racetrack) In his Progressive Dichotomy Paradox, Zeno argued that a runner will never reach the stationary goal line of a racetrack. The reason is that the runner must first reach half the distance to the goal, but when there he must still cross half the remaining distance to the goal, but having done that the runner must cover half of the new remainder, and so on. If the goal is one meter away, the runner must cover a distance of 1/2 meter, then 1/4 meter, then 1/8 meter, and so on ad infinitum. The runner cannot reach the final goal, says Zeno. Why not? There are few traces of Zeno's reasoning here, but for reconstructions that give the strongest reasoning, we may say that the runner will not reach the final goal because there is too far to run, the sum is actually infinite. The Standard Solution argues instead that the sum of this infinite geometric series is one, not infinity. Suppose Homer wishes to walk to the end of a path. Before he can get there, he must get halfway there. Before he can get halfway there, he must get a quarter of the way there. Before traveling a quarter, he must travel one-eighth; before an eighth, one-sixteenth; and so on. This description requires one to complete an infinite number of tasks, which Zeno maintains is an impossibility. The dichotomy This sequence also presents a second problem in that it contains no first distance to run, for any possible (finite) first distance could be divided in half, and hence would not be first after all. Hence, the trip cannot even begin. The paradoxical conclusion then would be that travel over any finite distance can neither be completed nor begun, and so all motion must be an illusion. An alternative conclusion, proposed by Henri Bergson, is that motion (time and distance) is not actually divisible. This argument is called the Dichotomy because it involves repeatedly splitting a distance into two parts. It contains some of the same elements as the Achilles and the Tortoise paradox, but with a more apparent conclusion of motionlessness. It is also known as the Race Course paradox. Some, like Aristotle, regard the Dichotomy as really just another version of Achilles and the Tortoise.[11] There are two versions of the dichotomy paradox. In the other version, before Homer could reach the end of the path, he must reach half of the distance to it. Before reaching the last half, he must complete the next quarter of the distance. Reaching the next quarter, he must then cover the next eighth of the distance, then the next sixteenth, and so on. There are thus an infinite number of steps that must first be accomplished before he could reach the end of the path. Expressed this way, the dichotomy paradox is very much analogous to that of Achilles and the tortoise.