Release Message:  Can one intend to drink the non-deadly toxin, if the intention is the only thing needed to get the reward? Authored by Gregory S. Kavka.

Description:  Can one intend to drink the non-deadly toxin, if the intention is the only thing needed to get the reward? Kavka's Toxin Puzzle Kavka's toxin puzzle is a thought experiment about the possibility of forming an intention to perform an act which, following from reason, is an action one would not actually perform. It was presented by moral and political philosopher Gregory S. Kavka in "The Toxin Puzzle" (1983), and grew out of his work in deterrence theory and mutual assured destruction.

Release Message:  Certain systems of formal logic are inconsistent. Authored by Stephen Kleene and J. B. Roser.

Description:  In mathematics, the Kleene-Rosser paradox is a paradox that shows that certain systems of formal logic are inconsistent, in particular the version of Curry's combinatory logic introduced in 1930, and Church's original lambda calculus, introduced in 1932-1933, both originally intended as systems of formal logic. The paradox was exhibited by Stephen Kleene and J. B. Rosser in 1935.

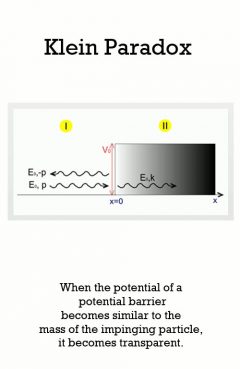
Release Message:  When the potential of a potential barrier becomes similar to the mass of the impinging particle, it becomes transparent. Authored by Oskar Benjamin Klein.

Description:  In 1929, physicist Oskar Klein obtained a surprising result by applying the Dirac equation to the familiar problem of electron scattering from a potential barrier. In nonrelativistic quantum mechanics, electron tunneling into a barrier is observed, with exponential damping. However, Klein's result showed that if the potential is on the order of the electron mass, V _ mc2, the barrier is nearly transparent. Moreover, as the potential approaches infinity, the reflection diminishes and the electron is always transmitted.

Release Message:  If it is provable in F that "if P is provable in F then P is true", then P is provable in F.

Description:  L ob did research on proof theory, modal logic and computability theory. He formulated L ob's theorem in 1955, as a formal version of L ob's paradox, that any statement that states that assert their own provability must be true (similar to G odel's incompleteness theorem).

Release Message:  A ladder fits inside a garage which would normally be too small to contain it.

Description:  The ladder paradox (or barn-pole paradox) is a thought experiment in special relativity. It involves a ladder, parallel to the ground, traveling horizontally and therefore undergoing a Lorentz length contraction. As a result, the ladder fits inside a garage which would normally be too small to contain it. On the other hand, from the point of view of an observer moving with the ladder, it is the garage that is moving, so it is the garage which will be contracted to an even smaller size, thus being unable to contain the ladder. This apparent paradox results from the mistaken assumption of absolute simultaneity. The ladder fits into the garage only if both of its ends are simultaneously inside the garage. In relativity, simultaneity is relative to each observer, and so the question of whether the ladder fits inside the garage is relative to each observer, and the paradox is resolved.

Release Message:  Every part of any plurality is both so small as to have no size but also so large as to be infinite.

Description:  Suppose there exist many things rather than, as Parmenides says, just one thing. Then every part of any plurality is both so small as to have no size but also so large as to be infinite, says Zeno. His reasoning for why they have no size has been lost, but many commentators suggest that he'd reason as follows. If there is a plurality, then it must be composed of parts which are not themselves pluralities. Yet things that are not pluralities cannot have a size or else they'd be divisible into parts and thus be pluralities themselves. Now, why are the parts of pluralities so large as to be infinite? Well, the parts cannot be so small as to have no size since adding such things together would never contribute anything to the whole so far as size is concerned. So, the parts have some non-zero size. If so, then each of these parts will have two spatially distinct sub-parts, one in front of the other. Each of these sub-parts also will have a size. The front part, being a thing, will have its own two spatially distinct sub-parts, one in front of the other; and these two sub-parts will have sizes. Ditto for the back part. And so on without end. A sum of all these sub-parts would be infinite. Therefore, each part of a plurality will be so large as to be infinite.

Release Message:  The Legends track down an anachronism in 1930s Hollywood, where Helen of Troy has started a war between two film studios. Starring Brandon Routh as Ray Palmer.

Description:  The Legends track down an anachronism in 1930s Hollywood, where Helen of Troy has started a war between two film studios.

Release Message:  Some countries export labor-intensive commodities and import capital-intensive commodities, in contradiction with Heckscher_Ohlin theory. Authored by Wassily Leontief.

Description:  Leontief's paradox in economics is that the country with the world's highest capital-per worker has a lower capital/labor ratio in exports than in imports. This econometric find was the result of Professor Wassily W. Leontief's attempt to test the Heckscher-Ohlin theory empirically. In 1954, Leontief found that the U.S. (the most capital-abundant country in the world) exported labor-intensive commodities and imported capital-intensive commodities, in contradiction with Heckscher-Ohlin theory ("H-O theory").

Release Message:  The length of time that it takes for a protein chain to find its folded state is many orders of magnitude shorter than it would be if it freely searched all possible configurations. Discovered by Cyrus Levinthal.

Description:  Levinthal's paradox is a thought experiment, also constituting a self-reference in the theory of protein folding. In 1969, Cyrus Levinthal noted that, because of the very large number of degrees of freedom in an unfolded polypeptide chain, the molecule has an astronomical number of possible conformations. An estimate of 3300 or 10143 was made in one of his papers.[1] (Often incorrectly cited as a 1968 paper.[2]) For example, a polypeptide of 100 residues will have 99 peptide bonds, and therefore 198 different phi and psi bond angles. If each of these bond angles can be in one of three stable conformations, the protein may misfold into a maximum of 3198 different conformations (including any possible folding redundancy). Therefore if a protein were to attain its correctly folded configuration by sequentially sampling all the possible conformations, it would require a time longer than the age of the universe to arrive at its correct native conformation. This is true even if conformations are sampled at rapid (nanosecond or picosecond) rates. The "paradox" is that most small proteins fold spontaneously on a millisecond or even microsecond time scale. This paradox is central to computational approaches to protein structure prediction.[3] Levinthal himself was aware that proteins fold spontaneously and on short timescales. He suggested that the paradox can be resolved if "protein folding is sped up and guided by the rapid formation of local interactions which then determine the further folding of the peptide; this suggests local amino acid sequences which form stable interactions and serve as nucleation points in the folding process."[4] Indeed, the protein folding intermediates and the partially folded transition states were experimentally detected, which explains the fast protein folding. This is also described as protein folding directed within funnel-like energy landscapes[5][6][7] Some computational approaches to protein structure prediction have sought to identify and simulate the mechanism of protein folding.[8] Levinthal also suggested that the native structure might have a higher energy, if the lowest energy was not kinetically accessible. An analogy is a rock tumbling down a hillside that lodges in a gully rather than reaching the base.[9]

Release Message:  "Everything I say is a lie."

Description:  The Liar (pseudomenos) paradox: A man says: "What I am saying now is a lie." If the statement is true, then he is lying, even though the statement is true. If the statement is a lie, then he is not actually lying, even though the statement is a lie. Thus, if the speaker is lying, he tells the truth, and vice versa.

Release Message:  "Minimal Liberty" is incompatible with Pareto optimality.

Description:  "Minimal Liberty" is incompatible with Pareto optimality. The liberal paradox, also Sen paradox or Sen's paradox, is a logical paradox discovered by Amartya Sen which purports to show that no social system can simultaneously 1 be committed to a minimal sense of freedom, 2 always result in a type of economic efficiency known as Pareto efficiency, and 3 be capable of functioning in any society whatsoever.

Release Message:  "I have a map of the United States... Actual size. It says, 'Scale: 1 mile = 1 mile.' I spent last summer folding it. I hardly ever unroll it. People ask me where I live, and I say, 'E6."

Description:  "I have a map of the United States... Actual size. It says, 'Scale: 1 mile = 1 mile.' I spent last summer folding it. I hardly ever unroll it. People ask me where I live, and I say, 'E6."

Release Message: 

Description: 

Release Message:  There are many things, but a fixed number, and so they will be ñlimited.î But given many things, each two must be distinct with a third thing separating them, so they will be ñunlimited.î

Description:  This paradox is alsoæcalled the Paradox of Denseness.æSuppose there exist many things rather than, as Parmenides would say, just one thing. Then there will be a definite or fixed number of those many things, and so they will be ñlimited.î But if there are many things, say two things, then they must be distinct, and to keep them distinct there must be a third thing separating them. So, there are three things. But between these, ƒ. In other words, things are dense and there is no definite or fixed number of them, so they will be ñunlimited.î This is a contradiction, because the plurality would be both limited and unlimited. Therefore, there are no pluralities; there exists only one thing, not many things. This argument is reconstructed from Zeno's own words, as quoted by Simplicius in his commentary of book 1 of Aristotle's Physics. According to the Standard Solution to this paradox, the weakness of Zeno's argument can be said to lie in the assumption that ñto keep them distinct, there must be a third thing separating them.î Zeno would have been correct to say that between any two physical objects that are separated in space, there is a place between them, because space is dense, but he is mistaken to claim that there must be a third physical object there between them. Two objects can be distinct at a time simply by one having a property the other does not have.

Release Message:  Tiny errors in the null hypothesis are magnified when large data sets are analyzed, leading to false but highly statistically significant results. Authored by Dennis Lindley.

Description:  Lindley's paradox is a counterintuitive situation in statistics in which the Bayesian and frequentist approaches to a hypothesis testing problem give different results for certain choices of the prior distribution. The problem of the disagreement between the two approaches was discussed in Harold Jeffreys' textbook;[1] it became known as Lindley's paradox after Dennis Lindley called the disagreement a paradox in a 1957 paper.[2] Although referred to as a paradox, the differing results from the Bayesian and Frequentist approaches can be explained as using them to answer fundamentally different questions, rather than actual disagreement between the two methods.

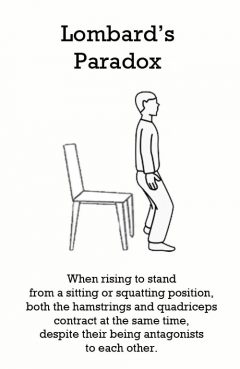
Release Message:  When rising to stand from a sitting or squatting position, both the hamstrings and quadriceps contract at the same time, despite their being antagonists to each other. Authored by Warren Lombard.

Description:  When rising to stand from a sitting or squatting position, both the hamstrings and quadriceps contract at the same time, despite their being antagonists to each other. Lombard's Paradox describes a paradoxical muscular contraction in humans. When rising to stand from a sitting or squatting position, both the hamstrings and quadriceps contract at the same time, despite their being antagonists to each other. The rectus femoris biarticular muscle acting over the hip has a smaller hip moment arm than the hamstrings. However, the rectus femoris moment arm is greater over the knee than the hamstring knee moment. This means that contraction from both rectus femoris and hamstrings will result in hip and knee extension. Hip extension also adds a passive stretch component to rectus femoris, which results in a knee extension force. This paradox allows for efficient movement, especially during gait.

Release Message:  Why is there an inevitable increase in entropy when the laws of physics are invariant under time reversal? The time reversal symmetry of physical laws appears to contradict the second law of thermodynamics. Conceived by Johann Josef Loschmidt.

Description:  Loschmidt's paradox, first published by Sir William Thomson, 1st Baron Kelvin, in 1874,[1] also known as the reversibility paradox, is the objection that it should not be possible to deduce an irreversible process from time-symmetric dynamics. This puts the time reversal symmetry of (almost) all known low-level fundamental physical processes at odds with any attempt to infer from them the second law of thermodynamics which describes the behaviour of macroscopic systems. Both of these are well-accepted principles in physics, with sound observational and theoretical support, yet they seem to be in conflict; hence the paradox. Johann Loschmidt's criticism was provoked by the H-theorem of Boltzmann, which was an attempt to explain using kinetic theory the increase of entropy in an ideal gas from a non-equilibrium state, when the molecules of the gas are allowed to collide. In 1876, Loschmidt pointed out that if there is a motion of a system from time t0 to time t1 to time t2 that leads to a steady decrease of H (increase of entropy) with time, then there is another allowed state of motion of the system at t1, found by reversing all the velocities, in which H must increase. This revealed that one of Boltzmann's key assumptions, molecular chaos, or, the Stosszahlansatz, that all particle velocities were completely uncorrelated, did not follow from Newtonian dynamics. One can assert that possible correlations are uninteresting, and therefore decide to ignore them; but if one does so, one has changed the conceptual system, injecting an element of time-asymmetry by that very action. Reversible laws of motion cannot explain why we experience our world to be in such a comparatively low state of entropy at the moment (compared to the equilibrium entropy of universal heat death); and to have been at even lower entropy in the past.

Release Message:  It is philosophically justifiable to believe that every individual lottery ticket won't win, but not justifiable to believe that no lottery ticket will win. Authored by Henry E. Kyburg, Jr.

Description:  Henry E. Kyburg, Jr.'s lottery paradox (1961, p. 197) arises from considering a fair 1000 ticket lottery that has exactly one winning ticket. If this much is known about the execution of the lottery it is therefore rational to accept that some ticket will win. Suppose that an event is very likely only if the probability of it occurring is greater than 0.99. On these grounds it is presumed rational to accept the proposition that ticket 1 of the lottery will not win. Since the lottery is fair, it is rational to accept that ticket 2 won't win either--indeed, it is rational to accept for any individual ticket i of the lottery that ticket i will not win. However, accepting that ticket 1 won't win, accepting that ticket 2 won't win, and so on until accepting that ticket 1000 won't win: that entails that it is rational to accept that no ticket will win, which entails that it is rational to accept the contradictory proposition that one ticket wins and no ticket wins. The lottery paradox was designed to demonstrate that three attractive principles governing rational acceptance lead to contradiction, namely that It is rational to accept a proposition that is very likely true, It is irrational to accept a proposition that is known to be inconsistent, and If it is rational to accept a proposition A and it is rational to accept another proposition A', then it is rational to accept A & A', are jointly inconsistent. The paradox remains of continuing interest because it raises several issues at the foundations of knowledge representation and uncertain reasoning: the relationships between fallibility, corrigible belief and logical consequence; the roles that consistency, statistical evidence and probability play in belief fixation; the precise normative force that logical and probabilistic consistency have on rational belief.

Release Message:  Most intimate relationships are based on love but also involve romantic compromises.

Description:  The love paradox in current society arises from a combination of the following two seemingly opposing claims: (a) a greater percentage of intimate relationships are based on love; (b) a greater percentage of intimate relationships involve romantic compromises. Since romantic compromises are considered to run counter to love, how can these two claims co-exist?

Release Message:  Low birth-weight children born to smoking mothers have a lower infant mortality rate than the low birth weight children of non-smokers. Authored by Allen J. Wilcox.

Description:  Low birth weight and mothers who smoke contribute to a higher mortality rate. Babies of smokers have lower average birth weight, but low birth weight babies born to smokers have a lower mortality rate than other low birth weight babies. (A special case of Simpson's paradox.)