Release Message:  You travel back in time and kill a famous person in history before they become famous; but if the person had never been famous then he could not have been targeted as a famous person.

Description:  You travel back in time and kill a famous person in history before they become famous; but if the person had never been famous then he could not have been targeted as a famous person.

Release Message:  A free choice in which only one option is offered. Authored by Thomas Hobson.

Description:  A free choice in which only one option is offered. As a person may refuse to take that option, the choice is therefore between taking the option or not; "take it or leave it". The phrase is said to originate with Thomas Hobson (1544-1631), a livery stable owner in Cambridge, England. To rotate the use of his horses, he offered customers the choice of either taking the horse in the stall nearest the door or taking none at all.

Release Message:  The amount of information that can be stored in a given volume is not proportional to the volume but to the area that bounds that volume.

Description:  The amount of information that can be stored in a given volume is not proportional to the volume but to the area that bounds that volume.

Release Message:  What you have not lost, you have. But you have not lost horns. Therefore you have horns. Authored by Eubulides.

Description:  The Horns (keratin s) paradox: What you have not lost, you have. But you have not lost horns. Therefore you have horns.

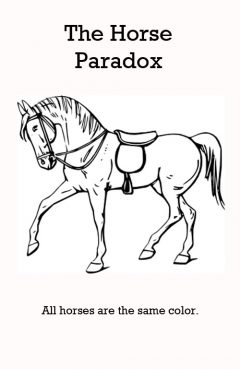
Release Message:  All horses are the same color. Authored by Joel C. Cohen.

Description:  Assume that horses always are the same color. Let us consider a group consisting of horses. First, exclude the last horse and look only at the first horses; all these are the same color since horses always are the same color. Likewise, exclude the first horse and look only at the last horses. These too, must also be of the same color. Therefore, the first horse in the group is of the same color as the horses in the middle, who in turn are of the same color as the last horse. Hence the first horse, middle horses, and last horse are all of the same color, and we have proven that: If horses have the same color, then horses will also have the same color. We already saw in the base case that the rule ("all horses have the same color") was valid for . The inductive step showed that since the rule is valid for , it must also be valid for , which in turn implies that the rule is valid for and so on. Thus in any group of horses, all horses must be the same color.[2]

Release Message:  In any society, the population submits to the rulers, even though force is always in the hands of the governed.

Description:  in any society, the population submits to the rulers, even though force is always in the hands of the governed.

Release Message:  If asking oneself "Am I dreaming?" in a dream proves that one is, what does it prove in waking life? Authored by Eric Bond Hutton.

Description:  If asking oneself "Am I dreaming?" in a dream proves that one is, what does it prove in waking life? An intriguing paradox concerning dreams and the nature of reality was described by the British writer Eric Bond Hutton in 1989. As a child Hutton often had lucid dreams in which people and things seemed as solid and real as in waking life. This led him to wonder whether life itself was a dream, even whether he existed only in somebody else's dream. Once in a while he would have a pre-lucid dream (in which one suspects that one is dreaming). He always found these somewhat disturbing, but one day hit upon a magic formula to be used in them: "If I find myself asking 'Am I dreaming?' it proves that I am, since this question would never occur to me in waking life." Yet, such is the nature of dreams, he could never recall it when he needed to. Many years later, when he came to write about his childhood fascination with dreams, he was struck by a contradiction in his earlier reasoning. True, asking oneself "Am I dreaming?" in a dream would seem to prove that one is. And yet that is precisely what he had often asked himself in waking life. Therein lay a paradox. What was he to conclude? That it does not prove one is dreaming, or that life really is a dream? The dream argument is the postulation that the act of dreaming provides preliminary evidence that the senses we trust to distinguish reality from illusion should not be fully trusted, and therefore any state that is dependent on our senses should at the very least be carefully examined and rigorously tested to determine whether it is in fact reality.

Release Message: 

Description: 

Release Message:  The pressure at a certain level in a fluid is proportional to the vertical distance to the surface of the liquid. Authored by Robert Boyle.

Description:  The pressure at a certain level in a fluid is proportional to the vertical distance to the surface of the liquid. Boyle's self-flowing flask, a perpetual motion machine, which appears to fill itself through siphon action ("hydrostatic perpetual motion") and involves the "hydrostatic paradox"[29] This is not possible in reality; a siphon requires its "output" to be lower than the "input".

Release Message:  Some businesses bring about their own downfall through their own successes.

Description:  Some businesses bring about their own downfall through their own successes.

Release Message: 

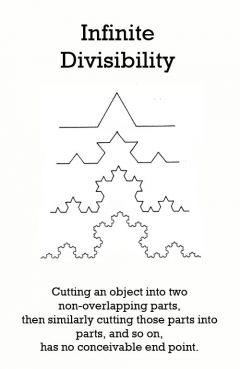
Description:  This is the most challenging of all the paradoxes of plurality. Consider the difficulties that arise if we assume that an object theoretically can be divided into a plurality of parts. According to Zeno, there is a reassembly problem. Imagine cutting the object into two non-overlapping parts, then similarly cutting these parts into parts, and so on until the process of repeated division is complete. Assuming the hypothetical division is ñexhaustiveî or does comes to an end, then at the end we reach what Zeno calls ñthe elements.î Here there is a problem about reassembly. There are three possibilities. (1) The elements are nothing. In that case the original objects will be a composite of nothing, and so the whole object will be a mere appearance, which is absurd. (2) The elements are something, but they have zero size. So, the original object is composed of elements of zero size. Adding an infinity of zeros yields a zero sum, so the original object had no size, which is absurd. (3) The elements are something, but they do not have zero size. If so, these can be further divided, and the process of division was not complete after all, which contradicts our assumption that the process was already complete. In summary, there were three possibilities, but all three possibilities lead to absurdity. So, objects are not divisible into a plurality of parts.

Release Message:  Why one will wait longer for a bus than one should.

Description:  Renewal theory is the branch of probability theory that generalizes Poisson processes for arbitrary holding times. Applications include calculating the best strategy for replacing worn-out machinery in a factory and comparing the long-term benefits of different insurance policies.

Release Message:  The first number that can be considered "dull" rather than "interesting" becomes interesting because of that fact.

Description:  The interesting number paradox is a semi-humorous paradox which arises from the attempt to classify natural numbers as "interesting" or "dull". The paradox states that all natural numbers are interesting. The "proof" is by contradiction: if there exists a non-empty set of uninteresting numbers, there would be a smallest uninteresting number -- but the smallest uninteresting number is itself interesting because it is the smallest uninteresting number, producing a contradiction.

Release Message:  An apparently correct mathematical derivation that leads to an obvious contradiction.

Description:  An apparently correct mathematical derivation that leads to an obvious contradiction.

Release Message:  It is easier to solve a more general problem that covers the specifics of the sought-after solution, than solving the actual problem.

Description:  It is easier to solve a more general problem that covers the specifics of the sought-after solution, than solving the actual problem.

Release Message:  What would happen if an unstoppable force hit an immovable object?

Description:  What would happen if an unstoppable force hit an immovable object?

Release Message: 

Description: 

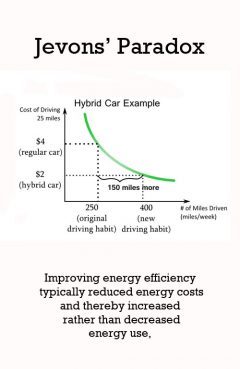
Release Message:  Increases in efficiency lead to even larger increases in demand. Authored by William Stanley Jevons.

Description:  In economics, the Jevons paradox (sometimes Jevons effect) is the proposition that technological progress that increases the efficiency with which a resource is used tends to increase (rather than decrease) the rate of consumption of that resource.[1] In 1865, the English economist William Stanley Jevons observed that technological improvements that increased the efficiency of coal use led to increased consumption of coal in a wide range of industries. He argued that, contrary to common intuition, technological improvements could not be relied upon to reduce fuel consumption.[2] The Jevons paradox was first described by the English economist William Stanley Jevons in his 1865 book The Coal Question.

Release Message: 

Description: 

Release Message:  An outcome is considered more efficient by arranging sufficient compensation from those that are made better off to those that are made worse off so that all would end up no worse off than before. Authored by Nicholas Kaldor and John Hicks.

Description:  Kaldor-Hicks efficiency, named for Nicholas Kaldor and John Hicks, also known as Kaldor-Hicks criterion, is a measure of economic efficiency that captures some of the intuitive appeal of Pareto efficiency, but has less stringent criteria and is hence applicable to more circumstances. Under Kaldor-Hicks efficiency, an outcome is considered more efficient if a Pareto optimal outcome can be reached by arranging sufficient compensation from those that are made better off to those that are made worse off so that all would end up no worse off than before.