Release Message:  Though most numbers are not squares, there are no more numbers than squares. Authored by Galileo Galilei.

Description:  Galileo's paradox is a demonstration of one of the surprising properties of infinite sets. In his final scientific work, Two New Sciences, Galileo Galilei made apparently contradictory statements about the positive integers. First, some numbers are squares, while others are not; therefore, all the numbers, including both squares and non-squares, must be more numerous than just the squares. And yet, for every square there is exactly one positive number that is its square root, and for every number there is exactly one square; hence, there cannot be more of one than of the other. This is an early use, though not the first, of the idea of one-to-one correspondence in the context of infinite sets. Galileo concluded that the ideas of less, equal, and greater apply to finite sets, but not to infinite sets. In the nineteenth century, using the same methods, Cantor showed that this restriction is not necessary. It is possible to define comparisons amongst infinite sets in a meaningful way (by which definition the two sets he considers, integers and squares, have "the same size"), and that by this definition some infinite sets are strictly larger than others. It is nonetheless remarkable the extent by which Galileo anticipated later work on infinite numbers. He showed that the number of points in a line segment is the same as the number in a larger line segment, but of course he didn't discover Cantor's proof that this is greater than the number of integers. Galileo had more urgent matters in mind. He was addressing the contradictions in Zeno's paradoxes in order to open the way for his mathematical theory of motion.[1] (Naive set theory)

Release Message:  In an ideal gas, is entropy an extensive variable?

Description:  In statistical mechanics, a semi-classical derivation of the entropy that does not take into account the indistinguishability of particles, yields an expression for the entropy which is not extensive (is not proportional to the amount of substance in question). This leads to a paradox known as the Gibbs paradox, after Josiah Willard Gibbs. The paradox allows for the entropy of closed systems to decrease, violating the second law of thermodynamics. It is possible, however, to take the perspective that it is merely the definition of entropy that is changed to ignore particle permutation (and thereby avert the paradox).

Release Message:  Why were interest rates and prices correlated? Authored by Alfred Herbert Gibson.

Description:  Gibson's Paradox is the observation that the rate of interest and the general level of prices are positively correlated.[1] It is named for British economist Alfred Herbert Gibson who noted the correlation in a 1923 article for Banker's Magazine. The correlation had been noted earlier by Thomas Tooke.[2] The term was first used by John Maynard Keynes, in his 1930 work, A Treatise on Money.[3] It was believed to be a paradox because most economic theorists predicted that the correlation would be negative. Keynes commented that the observed correlation was "one of the most completely established empirical facts in the whole field of quantitative economics."

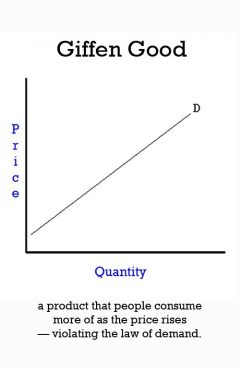
Release Message:  Increasing the price of bread makes poor people eat more of it. Authored by Sir Robert Giffen.

Description:  Increasing the price of bread makes poor people eat more of it. According to the Law of Demand, when the price of a commodity falls the demand for it rises. Giffen's Paradox is an exception to this law. It is named after the 19th century British economist, Sir Robert Giffen, who found that when the price of bread fell, the demand for it also fell. This was because when the price fell, the real income of the consumer rose and she was in a position to buy better quality/more bread. Named BY ____ Marshall

Release Message:  The large amount of glycogen in the liver cannot be explained by its small glucose absorption.

Description:  The large amount of glycogen in the liver cannot be explained by its small glucose absorption.

Release Message:  No consistent system of axioms whose theorems can be listed by an "effective procedure" is capable of proving all truths about the relations of the natural numbers, and such a system cannot demonstrate its own consistency. Authored by Kurt Friedrich G odel.

Description:  Godel's incompleteness theorems G odel's incompleteness theorems are two theorems of mathematical logic that establish inherent limitations of all but the most trivial axiomatic systems capable of doing arithmetic. The theorems, proven by Kurt G odel in 1931, are important both in mathematical logic and in the philosophy of mathematics. The two results are widely, but not universally, interpreted as showing that Hilbert's program to find a complete and consistent set of axioms for all mathematics is impossible, giving a negative answer to Hilbert's second problem. The first incompleteness theorem states that no consistent system of axioms whose theorems can be listed by an "effective procedure" (e.g., a computer program, but it could be any sort of algorithm) is capable of proving all truths about the relations of the natural numbers (arithmetic). For any such system, there will always be statements about the natural numbers that are true, but that are unprovable within the system. The second incompleteness theorem, an extension of the first, shows that such a system cannot demonstrate its own consistency.

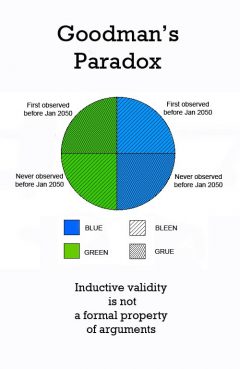
Release Message:  Why can induction be used to confirm that things are "green", but not to confirm that things are "grue"? Authored by Nelson Goodman.

Description:  Grue and Bleen Grue and bleen are predicates coined by Nelson Goodman in Fact, Fiction, and Forecast to illustrate "the new riddle of induction". These predicates are unusual because their application to things are time dependent. For Goodman they illustrate the problem of projectable predicates and ultimately, which empirical generalizations are law-like and which are not. Goodman's construction and use of grue and bleen illustrates how philosophers use simple examples in conceptual analysis.

Release Message:  A single grain of millet makes no sound upon falling, but a thousand grains make a sound. Authored by Zeno.

Description:  There are two common interpretations of this paradox. According to the first, which is the standard interpretation, when a bushel of millet (or wheat) grains falls out of its container and crashes to the floor, it makes a sound. Since the bushel is composed of individual grains, each individual grain also makes a sound, as should each thousandth part of the grain, and so on to its ultimate parts. But this result contradicts the fact that we actually hear no sound for portions like a thousandth part of a grain, and so we surely would hear no sound for an ultimate part of a grain. Yet, how can the bushel make a sound if none of its ultimate parts make a sound? The original source of this argument is Aristotle Physics, Book VII, chapter 4,æ250a19-21). There seems to be appeal to the iterative rule that if a millet or millet part makes a sound, then so should a next smaller part. Aristotle's refutation: Zeno is wrong in saying that there is no part of the millet that does not make a sound: for there is no reason why any such part should not in any length of time fail to move the air that the whole bushel moves in falling. In fact it does not of itself move even such a quantity of the air as it would move if this part were by itself: for no part even exists otherwise than potentially. Description of the paradox from the Routledge Dictionary of Philosophy: The argument is that a single grain of millet makes no sound upon falling, but a thousand grains make a sound. Hence a thousand nothings become something, an absurd conclusion.[17] Description from Nick Huggett: This is a Parmenidean argument that one cannot trust one's sense of hearing. Aristotle's response seems to be that even inaudible sounds can add to an audible sound.[18]

Release Message:  You travel back in time and kill your grandfather before he conceives one of your parents, which precludes your own conception and, therefore, you couldn't go back in time and kill your grandfather. Possibly originated by Rene Barjavel in his 1944 novel Le Voyager Imprudent.

Description:  You travel back in time and kill your grandfather before he conceives one of your parents, which precludes your own conception and, therefore, you couldn't go back in time and kill your grandfather. The grandfather paradox is a proposed paradox of time travel which results in an inconsistency through changing the past. The paradox is described as follows: a time traveller goes back in time and kills his grandfather, eliminating the possibility of one of the time traveler's parents ever coming into existence. As a result, the time traveller is never born. But if the time traveller is never born, then he does not travel through time and kill his grandfather, which means the time traveller is born after all, and he kills his grandfather, and so on "A Sound Of Thunder" is a science fiction short story by Ray Bradbury, first published in Collier's magazine in the June 28, 1952 issue. As of 1984 it was the most re-published science fiction story up to the present time. It is based on the concept termed the grandfather paradox of time travel first described by the science fiction writer Ren e Barjavel in his 1943 book Le Voyageur Imprudent.

Release Message:  A gravitational singularity (sometimes called a spacetime singularity) is a term used to describe the center of a black hole where gravity is thought to approach infinity. In the center of each black hole is a singularity, a point where infinite density develops as spacetime approaches it.

Description:  A gravitational singularity (sometimes called a spacetime singularity) is a term used to describe the center of a black hole where gravity is thought to approach infinity. In the center of each black hole is a singularity, a point where infinite density develops as spacetime approaches it.

Release Message:  Despite their relatively small muscle mass, dolphins can swim at high speeds and obtain large accelerations. Authored by Sir James Gray.

Description:  Gray's Paradox Gray's Paradox is a paradox posed in 1936 by British zoologist Sir James Gray. The paradox was to figure out how dolphins can obtain such high speeds and accelerations with what appears to be a small muscle mass. Gray made an estimate of the power a dolphin could exert based on its physiology, and concluded the power was insufficient to overcome the drag forces in water. He hypothesized that Dolphin's skin must have special anti-drag properties.[1] In 2008, researchers from Rensselaer Polytechnic Institute, West Chester University and the University of California, Santa Cruz used digital particle image velocimetry to prove Gray wrong.[2]

Release Message:  Policies intending to reduce future CO2 emissions may lead to increased emissions in the present. Authored by Hans-Werner Sinn.

Description:  Policies intending to reduce future CO2 emissions may lead to increased emissions in the present.

Release Message:  Is the word "heterological", meaning "not applicable to itself", a heterological word? Authored by Kurt Grelling, and Leonard Nelson.

Description:  The Grelling-Nelson paradox is a semantic self-referential paradox formulated in 1908 by Kurt Grelling and Leonard Nelson and sometimes mistakenly attributed to the German philosopher and mathematician Hermann Weyl. It is thus occasionally called Weyl's paradox as well as Grelling's paradox. It is closely analogous to several other well-known paradoxes, in particular the Barber paradox and Russell's paradox. Suppose one interprets the adjectives "autological" and "heterological" as follows: An adjective is autological (sometimes homological) if and only if it describes itself. For example "short" is autological, since the word "short" is short. "English," "unhyphenated" and "pentasyllabic" are also autological. An adjective is heterological if it does not describe itself. Hence "long" is a heterological word, as are "unwritten" and "monosyllabic". All adjectives, it would seem, must be either autological or heterological, for each adjective either describes itself, or it doesn't. Problems arise in a number of instances, however: Paradoxical cases The Grelling-Nelson paradox arises when we consider the adjective "heterological". One can ask: Is "heterological" a heterological word? If the answer is 'no', "heterological" is autological. This leads to a contradiction. In this case, "heterological" does not describe itself: it must be a heterological word. If the answer is 'yes', "heterological" is heterological. This again leads to a contradiction, because if the word "heterological" describes itself, it is autological. Is "heterological" a heterological word? no "heterological" is autological "heterological" describes itself "heterological" is heterological, contradiction yes "heterological" does not describe itself "heterological" is not heterological, contradiction.

Release Message:  High-energy cosmic rays have been observed that seem to violate the Greisen-Zatsepin-Kuzmin limit, which is a consequence of special relativity. Authored by Kenneth Greisen, Georgiy Timofeyevich Zatsepin, and Vadim Kuzmin.

Description:  The Greisen_Zatsepin_Kuzmin limit (GZK limit) is a theoretical upper limit on the energy of cosmic rays (high energy charged particles from space) coming from "distant" sources. The limit is 5_1019 eV, or about 8 joules. The limit is set by slowing-interactions of cosmic ray protons with the microwave background radiation over long distances (~163 million light-years). The limit is at the same order of magnitude as the upper limit for energy at which cosmic rays have experimentally been detected. For example, one ultra-high-energy cosmic ray has been detected which appeared to possess a record 50 joules (312 million TeV) of energy (about the same as the kinetic energy of a 60 mph baseball).

Release Message:  Can a particle and its antiparticle interact without annihilating each other? Authored by Lucien Hardy.

Description:  Hardy's paradox is a thought experiment in quantum mechanics devised by Lucien Hardy in which a particle and its antiparticle may interact without annihilating each other. Experiments using the technique of weak measurement have studied an interaction of polarized photons and these have demonstrated that the phenomenon does occur. However, the consequence of these experiments maintain only that past events can be inferred about after their occurrence as a probabilistic wave collapse. These weak measurements are considered to be an observation themselves, and therefore part of the causation of wave collapse, making the objective results only a probabilistic function rather than a fixed reality.

Release Message:  There exists a countable subset C of the sphere S such that S divided by C is equidecomposable with two copies of itself. Authored by Felix Hausdorff.

Description:  In mathematics, the Hausdorff paradox, named after Felix Hausdorff, states that if you remove a certain countable subset of the sphere S2, the remainder can be divided into three disjoint subsets A, B and C such that A, B, C and B -C are all congruent. In particular, it follows that on S2 there is no finitely additive measure defined on all subsets such that the measure of congruent sets is equal (because this would imply that the measure of A is both 1/3 and 1/2 of the non-zero measure of the whole sphere). The paradox was published in Mathematische Annalen in 1914 and also in Hausdorff's book, Grundz_ge der Mengenlehre, the same year. The proof of the much more famous Banach-Tarski paradox uses Hausdorff's ideas. This paradox shows that there is no finitely additive measure on a sphere defined on all subsets which is equal on congruent pieces. (Hausdorff first showed in the same paper the easier result that there is no countably additive measure defined on all subsets.) The structure of the group of rotations on the sphere plays a crucial role here - the statement is not true on the plane or the line. In fact, as was later shown by Banach,[1] it is possible to define an "area" for all bounded subsets in the Euclidean plane (as well as "length" on the real line) such that congruent sets will have equal "area". (This Banach measure, however, is only finitely additive, so it is not a measure in the full sense, but it equals the Lebesgue measure on sets for which the latter exists.) This implies that if two open subsets of the plane (or the real line) are equi-decomposable then they have equal area.

Release Message:  Since the universe is not infinitely old, it cannot be infinite in extent. Authored by Lord Kelvin, Hermann von Helmholtz. and William Rankine.

Description:  Since the universe is not infinitely old, it cannot be infinite in extent. Formulated in 1862 by Lord Kelvin, Hermann von Helmholtz and William John Macquorn Rankine,[1] the heat death paradox, also known as Clausius' paradox and thermodynamic paradox,[2] is a reductio ad absurdum argument that uses thermodynamics to show the impossibility of an infinitely old universe.

Release Message:  If a hotel with infinitely many rooms is full, it can still take in more guests. Authored by David Hilbert.

Description:  Hilbert's paradox of the Grand Hotel is a veridical paradox (a valid argument with a seemingly absurd conclusion, as opposed to a falsidical paradox, which is a seemingly valid demonstration of an actual contradiction) about infinite sets presented by David Hilbert in the 1920s, meant to illustrate certain counterintuitive properties of infinite sets. Consider a hypothetical hotel with a countably infinite number of rooms, all of which are occupied. One might be tempted to think that the hotel would not be able to accommodate any newly arriving guests, as would be the case with a finite number of rooms. (infinity)

Release Message:  The finding that Hispanics in the U.S. tend to have substantially better health than the average population in spite of what their aggregate socio-economic indicators predict.

Description:  The finding that Hispanics in the U.S. tend to have substantially better health than the average population in spite of what their aggregate socio-economic indicators predict.

Release Message:  We learn from history that we do not learn from history. Authored by Georg Hegel.

Description:  We learn from history that we do not learn from history.