Braess's Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
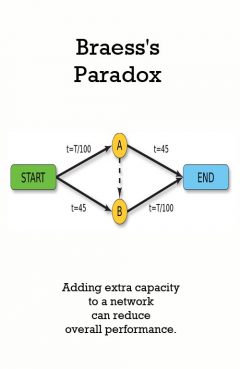
Release Message: Adding extra capacity to a network can reduce overall performance. Stated by Dietrich Braess.
Description: German mathematician Dietrich Braess, states that adding extra capacity to a network when the moving entities selfishly choose their route, can in some cases reduce overall performance. This is because the Nash equilibrium of such a system is not necessarily optimal. The paradox is stated as follows: "For each point of a road network, let there be given the number of cars starting from it, and the destination of the cars. Under these conditions one wishes to estimate the distribution of traffic flow. Whether one street is preferable to another depends not only on the quality of the road, but also on the density of the flow. If every driver takes the path that looks most favorable to him, the resultant running times need not be minimal. Furthermore, it is indicated by an example that an extension of the road network may cause a redistribution of the traffic that results in longer individual running times."
The Burali-Forti Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: If the ordinal numbers formed a set, it would be an ordinal number that is smaller than itself. Authored by Cesare Burali-Forti.
Description: In set theory, a field of mathematics, the Burali-Forti paradox demonstrates that naively constructing "the set of all ordinal numbers" leads to a contradiction and therefore shows an antinomy in a system that allows its construction. It is named after Cesare Burali-Forti, who discovered it in 1897. (Naive set theory)
Buridan's Ass
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: How can a rational choice be made between two outcomes of equal value? Authored by Jean Buridan.
Description: Buridan's ass is an illustration of a paradox in philosophy in the conception of free will. It refers to a hypothetical situation wherein an ass that is equally hungry and thirsty is placed precisely midway between a stack of hay and a pail of water. Since the paradox assumes the ass will always go to whichever is closer, it will die of both hunger and thirst since it cannot make any rational decision to choose one over the other. The paradox is named after the 14th century French philosopher Jean Buridan, whose philosophy of moral determinism it satirizes. A common variant of the paradox substitutes two identical piles of hay for the hay and water; the ass, unable to choose between the two, dies of hunger. Psychological / Philosophical
Buridan's Bridge
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Will Plato throw Socrates into the water or not? Authored by Jean Buridan.
Description: Buridan's Bridge (also known as Sophism 17) is described by Jean Buridan, one of the most famous and influential philosophers of the Late Middle Ages, in his book Sophismata. Sophism 17 is a self-referenced paradox that involves a proposition pronounced about an event that might or might not happen in the future. The sophism is: Imagine the following scenario: Socrates wants to cross a river and comes to a bridge guarded by Plato, who says: Plato: Socrates, if in the first proposition which you utter, you speak the truth, I will permit you to cross. But surely, if you speak falsely, I shall throw you into the water. Socrates: You will throw me into the water. Buridan's solution[edit] In order to solve the paradox Buridan proposes three questions: 1 Is the proposition uttered by Socrates: "You are going to throw me into the water" true, or is it false? 2 Is Plato's promise true or is it false? 3 "What ought Plato to do to fulfill his promise?"[3] In response to the first question Buridan states that it is impossible to determine if Socrates' proposition is true or false. This is because the proposition "You are going to throw me into the water" is a future contingent that could be true or false depending on what Plato is going to do. Dr. Joseph W. Ulatowski says that Buridan apparently used Aristotle's thesis about what "truth" is to come up with this response. Aristotle believed that a proposition is true if and only if it is verified by the state of things as they currently are. Contradicting the principle of bivalence, Buridan implies a system of three-valued logic in which there are three truth values--true, false, and some indeterminate third value.[3] In determining the truth value of Plato's conditional promise, Buridan suggests that Plato's promise was false, and that because Plato gave his promise carelessly he is not obligated to fulfill the promise.[3] In discussing the third question, "What ought Plato to do to fulfill his promise", Buridan states that Plato should not have given a conditional promise in the first place. He also suggests that Plato could have made sure that the condition was formulated in such a way that it would not cause a contradiction; because Plato cannot fulfill his conditional promise without violating it, he is not obligated to fulfill the promise. Ulatowski points out that this is the contrapositive of the principle stated by Immanuel Kant: "ought implies can".[3]
Buttered Cat Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: What would happen if one attached a piece of buttered toast (butter side up) to the back of a cat, then dropped the cat from a large height.
Description: The buttered cat paradox is a common joke based on the tongue-in-cheek combination of two adages: ´ Cats always land on their feet. ´ Buttered toast always lands buttered side down. The paradox arises when one considers what would happen if one attached a piece of buttered toast (butter side up) to the back of a cat, then dropped the cat from a large height. The buttered cat paradox, submitted by artist John Frazee of Kingston, New York, won a 1993 OMNI magazine competition about paradoxes. The idea may not have originated from Frazee since it had appeared on USENET by May 1992, if not before.[3]
The Butterfly Effect
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: In chaos theory, the butterfly effect is the sensitive dependence on initial conditions in which a small change in one state of a deterministic nonlinear system can result in large differences in a later state. Coined by Edward Norton Lorenz
Description: In chaos theory, the butterfly effect is the sensitive dependence on initial conditions in which a small change in one state of a deterministic nonlinear system can result in large differences in a later state. The name, coined by Edward Lorenz for the effect which had been known long before, is derived from the metaphorical example of the details of a hurricane (exact time of formation, exact path taken) being influenced by minor perturbations such as the flapping of the wings of a distant butterfly several weeks earlier. Lorenz discovered the effect when he observed that runs of his weather model with initial condition data that was rounded in a seemingly inconsequential manner would fail to reproduce the results of runs with the unrounded initial condition data. A very small change in initial conditions had created a significantly different outcome.
Cantor's Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: There is no greatest cardinal number, so the collection of "infinite sizes" is itself infinite. Thus, not only are there infinitely many infinities, but this infinity is larger than any of the infinities it enumerates. Authored by Georg Cantor.
Description: In set theory, Cantor's paradox is derivable from the theorem that there is no greatest cardinal number, so that the collection of "infinite sizes" is itself infinite. The difficulty is handled in axiomatic set theory by declaring that this collection is not a set but a proper class; in von Neumann_Bernays_G_del set theory it follows from this and the axiom of limitation of size that this proper class must be in bijection with the class of all sets. Thus, not only are there infinitely many infinities, but this infinity is larger than any of the infinities it enumerates. This paradox is named for Georg Cantor, who is often credited with first identifying it in 1899 (or between 1895 and 1897). Like a number of "paradoxes" it is not actually contradictory but merely indicative of a mistaken intuition, in this case about the nature of infinity and the notion of a set. Put another way, it is paradoxical within the confines of na¥ve set theory and therefore demonstrates that a careless axiomatization of this theory is inconsistent. (Naive set theory)
The Card Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: A card with these statements printed, one on each side: "The next statement is true. The previous statement is false." Authored by Philip Jourdain.
Description: The card paradox is a non-self-referential variant of the liar paradox constructed by Philip Jourdain.[1] It is also known as the postcard paradox, Jourdain paradox or Jourdain's paradox.
Carroll's Paradox (What the Tortoise Said to Achilles)
Release Date: //1895
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: What the Tortoise Said to Achilles "Whatever Logic is good enough to tell me is worth writing down...," also known as Carroll's paradox. Authored by Lewis Carroll.
Description: "What the Tortoise Said to Achilles", written by Lewis Carroll in 1895 for the philosophical journal Mind, is a brief dialogue which problematises the foundations of logic. The title alludes to one of Zeno's paradoxes of motion, in which Achilles could never overtake the tortoise in a race. In Carroll's dialogue, the tortoise challenges Achilles to use the force of logic to make him accept the conclusion of a simple deductive argument. Ultimately, Achilles fails, because the clever tortoise leads him into an infinite regression.
Carroll's Paradox (physics)
Release Date: //1984
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: The angular momentum of a stick should be zero, but is not. Authored by Michael M. Carroll.
Description: In physics, Carroll's paradox arises when considering the motion of a falling rigid rod that is specially constrained. Considered one way, the angular momentum stays constant; considered in a different way, it changes. It is named after Michael M. Carroll who first published it in 1984.
Catch-22
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: A situation in which someone is in need of something that can only be had by not being in need of it. Authored by Joseph Heller.
Description: In need of something which can only be had by not being in need of it There was only one catch and that was Catch-22, which specified that a concern for one's safety in the face of dangers that were real and immediate was the process of a rational mind. Orr was crazy and could be grounded. All he had to do was ask; and as soon as he did, he would no longer be crazy and would have to fly more missions. Orr would be crazy to fly more missions and sane if he didn't, but if he were sane he had to fly them. If he flew them he was crazy and didn't have to; but if he didn't want to he was sane and had to. Yossarian was moved very deeply by the absolute simplicity of this clause of Catch-22 and let out a respectful whistle. (p. 56, ch. 5)
Chain Store Paradox
Release Date: //1978
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Even those who know better play the so-called chain store game in an irrational manner. Authored by Reinhard Selten.
Description: The chain store game is a simple game in extensive form which produces an inconsistency between game theoretical reasoning and plausible human behavior. Well-informed players must be expected to disobey game theoretical recommendations. If Player A follows the game theory payoff matrix to achieve the optimal payoff, he or she will have a lower payoff than with the "deterrence" strategy. This creates an apparent game theory paradox: game theory states that induction strategy should be optimal, but it looks like "deterrence strategy" is optimal instead. The "deterrence strategy" is not a Nash equilibrium: It relies on the non-credible threat of responding to IN with AGGRESSIVE. A rational player will not carry out a non-credible threat, but the paradox is that it nevertheless seems to benefit Player A to carry out the threat.
Chicken or the Egg
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Which came first, the chicken or the egg?
Description: Aristotle (384_322 BC) was puzzled by the idea that there could be a first bird or egg and concluded that both the bird and egg must have always existed: If there has been a first man he must have been born without father or mother _ which is repugnant to nature. For there could not have been a first egg to give a beginning to birds, or there should have been a first bird which gave a beginning to eggs; for a bird comes from an egg.
Coastline Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
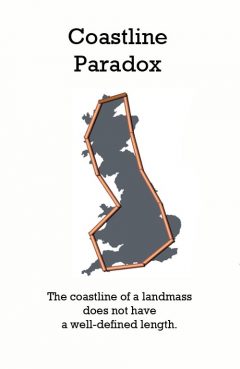
Release Message: The perimeter of a landmass is in general ill-defined. Authored by Lewis Fry Richardson.
Description: The coastline paradox is the counterintuitive observation that the coastline of a landmass does not have a well-defined length. This results from the fractal-like properties of coastlines. The first recorded observation of this phenomenon was by Lewis Fry Richardson and it was expanded by Benoit Mandelbrot. More concretely, the length of the coastline depends on the method used to measure it. Since a landmass has features at all scales, from hundreds of kilometres in size to tiny fractions of a millimetre and below, there is no obvious size of the smallest feature that should be measured around, and hence no single well-defined perimeter to the landmass. Various approximations exist when specific assumptions are made about minimum feature size.
The Code-talker Paradox
Release Date: //2001
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: A code-talker paradox is a situation in which a language prevents communication. How can a language both enable communication and block communication? Authored by Mark C. Baker.
Description: The term code-talker paradox was coined in 2001 by Mark Baker to describe the Navajo code talking used during World War II. Code talkers are able to create a language mutually intelligible to each other but completely unintelligible to everyone who does not know the code. This causes a conflict of interests without actually causing any conflict at all. In the case of Navajo code-talkers, cryptanalysts were unable to decode messages in Navajo, even when using the most sophisticated methods available. At the same time, the code talkers were able to encrypt and decrypt messages quickly and easily by translating them into and from Navajo. Thus the code talker paradox refers to how human languages can be so similar and different at once: so similar that one can learn them both and gain the ability to translate from one to the other, yet so different that if someone knows one language but does not know another, it is not always possible to derive the meaning of a text by analyzing it or infer it from the other language.
Condorcet Voting Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Collective preferences can be cyclic (i.e., not transitive), even if the preferences of individual voters are not cyclic. Authored by Marquis de Condorcet.
Description: The voting paradox (also known as Condorcet's paradox or the paradox of voting) is a situation noted by the Marquis de Condorcet in the late 18th century, in which collective preferences can be cyclic (i.e., not transitive), even if the preferences of individual voters are not cyclic.
Control Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Man can never be free of control, for to be free of control is to be controlled by oneself.
Description: Man can never be free of control, for to be free of control is to be controlled by oneself. On a personal level, it refers to the phenomenon by which the harder a person tries to control something, the more difficult it becomes to exercise that control. Examples that are often given of this phenomenon are: (1) the harder you try to fall a sleep, the more difficulty you have actually falling asleep; (2) the harder you try to stop thinking about something, the more you think about it; (3) the more you try to control negative emotions such as fear, the more powerful those emotions become.
Cool Tropics Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: A contradiction between modeled estimates of tropical temperatures during warm, ice-free periods of the Cretaceous and Eocene, and the colder temperatures that proxies suggest were present.
Description: A contradiction between modeled estimates of tropical temperatures during warm, ice-free periods of the Cretaceous and Eocene, and the colder temperatures that proxies suggest were present.
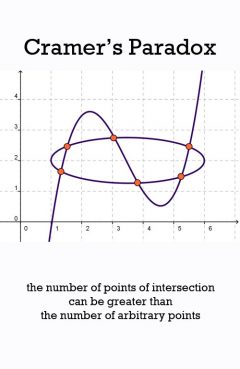
Cramer's Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: The number of points of intersection of two higher-order curves can be greater than the number of arbitrary points needed to define one such curve. Authored by Gabriel Cramer.
Description: In mathematics, Cramer's paradox is the statement that the number of points of intersection of two higher-order curves can be greater than the number of arbitrary points that are usually needed to define one such curve. It is named after the Swiss mathematician Gabriel Cramer. It has become known as Cramer's paradox after featuring in his 1750 book Introduction l'analyse des lignes courbes alg briques, although Cramer quoted Maclaurin as the source of the statement
The Crocodile Dilemma
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: If a crocodile steals a child and promises its return him if the father can correctly guess exactly what the crocodile will do, how should the crocodile respond in the case that the father correctly guesses that the child will not be returned?
Description: The transaction is logically smooth but unpredictable if the father guesses that the child will be returned, but a dilemma arises for the crocodile if he guesses that the child will not be returned. In the case that the crocodile decides to keep the child, he violates his terms: the father's prediction has been validated, and the child should be returned. However, in the case that the crocodile decides to give back the child, he still violates his terms, even if this decision is based on the previous result: the father's prediction has been falsified, and the child should not be returned. The question of what the crocodile should do is therefore paradoxical, and there is no justifiable solution. The crocodile dilemma serves to expose some of the logical problems presented by metaknowledge. In this regard, it is similar in construction to the unexpected hanging paradox, which Richard Montague(1960) used to demonstrate that the following assumptions about knowledge are inconsistent when tested in combination:[2] (i) If is known to be true, then . (ii) It is known that (i). (iii) If implies , and is known to be true, then is also known to be true. It also bears similarities to the liar paradox. Ancient Greek sources were the first to discuss the crocodile dilemma.[1]