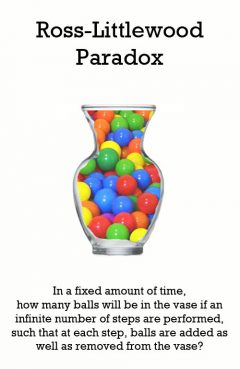Quine's (Liar) Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: "'Yields a falsehood when appended to its own quotation' yields a falsehood when appended to its own quotation." Authored by Willard Van Orman Quine.
Description: Quine's paradox is a paradox concerning truth values, attributed to Willard Van Orman Quine. It is related to the liar paradox as a problem, and it purports to show that a sentence can be paradoxical even if it is not self-referring and does not use demonstratives or indexicals (i.e. it does not explicitly refer to itself). The paradox can be expressed as follows: "Yields falsehood when preceded by its quotation" yields falsehood when preceded by its quotation. If the paradox is not clear, consider each part of the above description of the paradox incrementally: it = yields falsehood when preceded by its quotation its quotation = "yields falsehood when preceded by its quotation" it preceded by its quotation = "yields falsehood when preceded by its quotation" yields falsehood when preceded by its quotation. With these tools, we may now reconsider the description of the paradox. It can be seen to assert the following: The statement "'yields falsehood when preceded by its quotation' yields falsehood when preceded by its quotation" is false. In other words, the sentence implies that it is false, which is paradoxical -- for if it is false, what it states is in fact true.
The Raven Paradox (aka Hempel's paradox or Hempel's ravens)
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: All ravens are black. Authored by Carl Hempel.
Description: The Raven paradox, also known as Hempel's paradox or Hempel's ravens is a paradox arising from the question of what constitutes evidence for a statement. Observing objects that are neither black nor ravens may formally increase the likelihood that all ravens are black even though intuitively these observations are unrelated. Observing a green apple increases the likelihood of all ravens being black. This problem was proposed by the logician Carl Gustav Hempel in the 1940s to illustrate a contradiction between inductive logic and intuition. A related issue is the problem of induction and the gap between inductive and deductive reasoning.
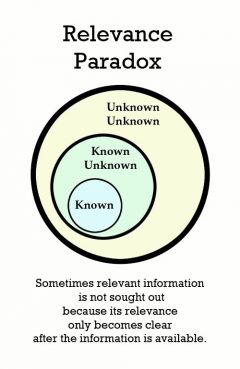
Relevance Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Sometimes relevant information is not sought out because its relevance only becomes clear after the information is available.
Description: Sometimes relevant information is not sought out because its relevance only becomes clear after the information is available.
Replacement Paradox
Richard's Paradox
Release Date: //1905
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: We appear to be able to use simple English to define a decimal expansion in a way that is self-contradictory. Authored by Jules Richard.
Description: In logic, Richard's paradox is a semantical antinomy in set theory and natural language first described by the French mathematician Jules Richard in 1905. Today, the paradox is ordinarily used in order to motivate the importance of carefully distinguishing between mathematics and metamathematics. The paradox was also a motivation in the development of predicative mathematics.
Rietdijk Putnam argument
Ross-Littlewood Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: In a fixed amount of time, how many balls will be in the vase if an infinite number of steps are performed, such that at each step, balls are added as well as removed from the vase?
Description: The Ross-Littlewood paradox (also known as the balls and vase problem or the ping pong ball problem) is a hypothetical problem in abstract mathematics and logic designed to illustrate the seemingly paradoxical, or at least non-intuitive, nature of infinity. More specifically, like the Thomson's lamp paradox, the Ross-Littlewood paradox tries to illustrate the conceptual difficulties with the notion of a supertask, in which an infinite number of tasks are completed sequentially.[1]
Russell's Paradox (aka Russell's Antimony)
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Does the set of all those sets that do not contain themselves contain itself? Authored by Bertrand Russell.
Description: A set containing all sets that are not members of themselves. According to naive set theory, any definable collection is a set. Let R be the set of all sets that are not members of themselves. If R is not a member of itself, then its definition dictates that it must contain itself, and if it contains itself, then it contradicts its own definition as the set of all sets that are not members of themselves. This contradiction is Russell's paradox. In the foundations of mathematics, Russell's paradox (also known as Russell's antinomy), discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction. The same paradox had been discovered a year before by Ernst Zermelo but he did not publish the idea, which remained known only to Hilbert, Husserl and other members of the University of G ttingen.
Russell's Paradox (mathematics)
SAR Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Exceptions to the principle that a small change in a molecule causes a small change in its chemical behavior are frequently profound.
Description: Exceptions to the principle that a small change in a molecule causes a small change in its chemical behavior are frequently profound.
Schrodinger's Cat Paradox (A quantum paradox)
Scitovsky Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Using the Kaldor_Hicks criterion, an allocation A may be more efficient than allocation B, while at the same time B is more efficient than A.
Description: The Scitovsky paradox is a theory which states that in welfare economics there is no increase in social welfare by a return to the original part of the losers. It is named after the Hungarian born American economist, Tibor Scitovsky. What he demonstrated was that if an allocation A is deemed superior to another allocation B by the Kaldor compensation criteria, by a subsequent set of moves by the same criteria, we can prove that B is also superior to A. The paradox occurs when the gainer from the change of allocation A to allocation B can compensate the loser for making the change, but the loser could also then compensate the gainer for going back to the original position.
Self-Absorption Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: The contradictory association whereby higher levels of self-awareness are simultaneously associated with higher levels of psychological distress and with psychological well-being.
Description: The contradictory association whereby higher levels of self-awareness are simultaneously associated with higher levels of psychological distress and with psychological well-being.
Service Recovery Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Successfully fixing a problem with a defective product may lead to higher consumer satisfaction than in the case where no problem occurred at all.
Description: Successfully fixing a problem with a defective product may lead to higher consumer satisfaction than in the case where no problem occurred at all.
Sherman Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: An anomalous pattern of inheritance in the fragile X syndrome.
Description: The Sherman Paradox refers to an anomalous pattern of inheritance found in Fragile X syndrome.[1] The phenomenon is also referred to as anticipation or dynamic mutation. The paradox is named after Stephanie Sherman, who studied the inheritance patterns of people with Fragile X syndrome. Sherman observed that the effects of Fragile X syndrome seemed to occur more frequently with each passing generation. This observation is now known as the Sherman Paradox. The paradox was ultimately explained by insights into the mutation process that gives rise to the syndrome. Sherman theorized that the gene responsible for Fragile X syndrome becomes mutated through a two-step process. The first mutation, called the 'premutation', doesn't cause any clinical symptoms. A second mutation was required to convert the 'premutation' into a 'full mutation' capable of causing the clinical symptoms associated with Fragile X syndrome. Additionally, premutations must pass through females in order to transform into the full mutation. The Fragile X syndrome is so named because of the appearance of the X chromosome in individuals with Fragile X. Under an electron microscope, a region on the long arm of the chromosome resembles a thin string. Investigation showed that this region consists of a CGG repeat triplet in both normal and diseased individuals.[1] The difference between normal and diseased is the length of the repeat; the repeat is longer where Fragile X syndrome is present. When the length of the repeat surpasses a critical threshold, symptoms of the disorder appear and they increase in likelihood and severity with further length. Even below this threshold there is a range where the repeat becomes unstable during meiosis. In normal individuals, an insertion of extra CGGs is unlikely. However, as the length of the repeat increases, the probability of additional triplet insertions increases. When the expansion reaches the danger range, the carrier is still unaffected, but the risk of further mutation becomes significant. This is called the premutation range. Once the Fragile X syndrome emerges, symptoms worsen from generation to generation because of the self promoting aspect of the mutation.
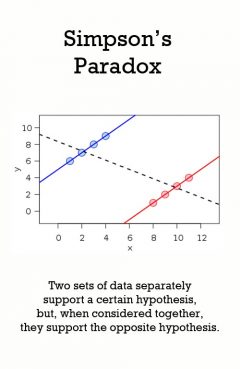
Simpson's Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: An association in sub-populations may be reversed in the population. Authored by Edward H. Simpson.
Description: In probability and statistics, Simpson's paradox, or the Yule-Simpson effect, is a paradox in which a trend that appears in different groups of data disappears when these groups are combined, and the reverse trend appears for the aggregate data. This result is often encountered in social-science and medical-science statistics,[1] and is particularly confounding when frequency data are unduly given causal interpretations.[2] Simpson's Paradox disappears when causal relations are brought into consideration. Though it is mostly unknown to laypeople, Simpson's paradox is well known to statisticians, and it is described in a few introductory statistics books.[3][4] Many statisticians believe that the mainstream public should be informed of the counter-intuitive results in statistics such as Simpson's paradox.[5][6] Edward H. Simpson first described this phenomenon in a technical paper in 1951,[7] but the statisticians Karl Pearson, et al., in 1899,[8] and Udny Yule, in 1903, had mentioned similar effects earlier.[9] The name Simpson's paradox was introduced by Colin R. Blyth in 1972.[10] Since Edward Simpson did not actually discover this statistical paradox (an instance of Stigler's law of eponymy), some writers, instead, have used the impersonal names reversal paradox and amalgamation paradox in referring to what is now called Simpson's Paradox and the Yule-Simpson effect.[11]
Simulation Paradox
Skolem's Paradox
Release Date: //1922
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Countably infinite models of set theory contain uncountably infinite sets. Authored by Thoralf Skolem.
Description: In mathematical logic and philosophy, Skolem's paradox is a seeming contradiction that arises from the downward L wenheim-Skolem theorem. Thoralf Skolem (1922) was the first to discuss the seemingly contradictory aspects of the theorem, and to discover the relativity of set-theoretic notions now known as non-absoluteness. Although it is not an actual antinomy like Russell's paradox, the result is typically called a paradox, and was described as a "paradoxical state of affairs" by Skolem (1922: p. 295). Skolem's paradox is that every countable axiomatisation of set theory in first-order logic, if it is consistent, has a model that is countable. This appears contradictory because it is possible to prove, from those same axioms, a sentence which intuitively says (or which precisely says in the standard model of the theory) that there exist sets that are not countable. Thus the seeming contradiction is that a model which is itself countable, and which contains only countable sets, satisfies the first order sentence that intuitively states "there are uncountable sets". A mathematical explanation of the paradox, showing that it is not a contradiction in mathematics, was given by Skolem (1922). Skolem's work was harshly received by Ernst Zermelo, who argued against the limitations of first-order logic, but the result quickly came to be accepted by the mathematical community. The philosophical implications of Skolem's paradox have received much study. One line of inquiry questions whether it is accurate to claim that any first-order sentence actually states "there are uncountable sets". This line of thought can be extended to question whether any set is uncountable in an absolute sense. More recently, the paper "Models and Reality" by Hilary Putnam, and responses to it, led to renewed interest in the philosophical aspects of Skolem's result.
Sleeping Beauty Problem
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: A probability problem that can be correctly answered as one half or one third depending on how the question is approached.
Description: The Sleeping Beauty problem is a puzzle in probability theory and formal epistemology in which an ideally rational epistemic agent is to be woken once or twice according to the toss of a coin, and asked her degree of belief for the coin having come up heads. The problem was originally formulated in unpublished work by Arnold Zuboff (this work was later published as "One Self: The Logic of Experience"[1]), followed by a paper by Adam Elga[2] but is based on earlier problems of imperfect recall and the older "paradox of the absentminded driver". Sleeping Beauty volunteers to undergo the following experiment and is told all of the following details: On Sunday she will be put to sleep. Once or twice, during the experiment, Beauty will be awakened, interviewed, and put back to sleep with an amnesia-inducing drug that makes her forget that awakening. A fair coin will be tossed to determine which experimental procedure to undertake: if the coin comes up heads, Beauty will be awakened and interviewed on Monday only. If the coin comes up tails, she will be awakened and interviewed on Monday and Tuesday. In either case, she will be awakened on Wednesday without interview and the experiment ends. Any time Sleeping Beauty is awakened and interviewed she will not be able to tell which day it is or whether she has been awakened before. During the interview Beauty is asked: "What is your credence now for the proposition that the coin landed heads?".
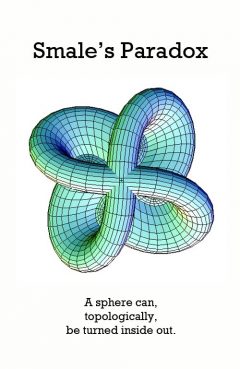
Smale's Paradox
Release Date: //1958
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: A sphere can, topologically, be turned inside out. Authored by Stephen Smale.
Description: In differential topology, Smale's paradox states that it is possible to turn a sphere inside out in a three-dimensional space with possible self-intersections but without creating any crease, a process more commonly and historically called sphere eversion (eversion means "to turn inside out"). This is surprising, to those who understand regular homotopy, and is hence deemed a veridical paradox.