Abilene Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: People can make decisions based not on what they actually want to do, but on what they think that other people want to do. Authored by Jerry B. Harvey.
Description: In an Abilene paradox a group of people collectively decide on a course of action that is counter to the preferences of many of the individuals in the group. Abilene paradox vs Accuracy paradox vs Prisoner's dilemma It involves a common breakdown of group communication in which each member mistakenly believes that their own preferences are counter to the group's and, therefore, does not raise objections. A common phrase relating to the Abilene paradox is a desire not to "rock the boat".
Absence Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: No one is ever "here".
Description: The absence paradox, while named a paradox, is more precisely an informal fallacy and humorous misuse of language which results in the conclusion that "No one is ever present." The statement of the argument is some formulation of the following: No person is ever present because he is either not in Rome or alternatively is not in Beijing. Therefore, he must be somewhere else. If he is somewhere else he is not here. The use of this fallacy dates from the 19th century. The fallacy in the argument is that it interprets the relative adverb "else" in an absolute sense.
The Accuracy Paradox
Release Date: //2007
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: The accuracy paradox for predictive analytics states that predictive models with a given level of accuracy may have greater predictive power than models with higher accuracy. Authored by Tilmann Bruckhaus.
Description: The accuracy paradox for predictive analytics states that predictive models with a given level of accuracy may have greater predictive power than models with higher accuracy. It may be better to avoid the accuracy metric in favor of other metrics such as precision and recall. [1] Accuracy is often the starting point for analyzing the quality of a predictive model, as well as an obvious criterion for prediction. Accuracy measures the ratio of correct predictions to the total number of cases evaluated. It may seem obvious that the ratio of correct predictions to cases should be a key metric. A predictive model may have high accuracy, but be useless.
Achilles and the Tortoise
Release Date: //-460
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: In a race, the quickest runner can never overtake the slowest, since the pursuer must first reach the point whence the pursued started, so that the slower must always hold a lead. Authored by Zeno.
Description: In the paradox of Achilles and the Tortoise, Achilles is in a footrace with the tortoise. Achilles allows the tortoise a head start of 100 meters, for example. If we suppose that each racer starts running at some constant speed (one very fast and one very slow), then after some finite time, Achilles will have run 100 meters, bringing him to the tortoise's starting point. During this time, the tortoise has run a much shorter distance, say, 10 meters. It will then take Achilles some further time to run that distance, by which time the tortoise will have advanced farther; and then more time still to reach this third point, while the tortoise moves ahead. Thus, whenever Achilles reaches somewhere the tortoise has been, he still has farther to go. Therefore, because there are an infinite number of points Achilles must reach where the tortoise has already been, he can never overtake the tortoise. In a race, the quickest runner can never overtake the slowest, since the pursuer must first reach the point whence the pursued started, so that the slower must always hold a lead. _ as recounted by Aristotle, Physics VI:9, 239b15
Alabama Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Increasing the total number of seats of government might shrink one block's seats.
Description: The Alabama paradox was the first of the apportionment paradoxes to be discovered. The US House of Representatives is constitutionally required to allocate seats based on population counts, which are required every 10 years. The size of the House is set by statute. After the 1880 census, C. W. Seaton, chief clerk of the United States Census Bureau, computed apportionments for all House sizes between 275 and 350, and discovered that Alabama would get 8 seats with a House size of 299 but only 7 with a House size of 300. In general the term Alabama paradox refers to any apportionment scenario where increasing the total number of items would decrease one of the shares. A similar exercise by the Census Bureau after the 1900 census computed apportionments for all House sizes between 350 and 400: Colorado would have received three seats in all cases, except with a House size of 357 in which case it would have received two.
Algol Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Some binary stars seem to have different ages, even though they're thought to have formed at the same time.
Description: In stellar astronomy, the Algol paradox is an apparently paradoxical situation when elements of a binary star seem to evolve in discord with the established theories of stellar evolution. A fundamental feature of these theories is that the rate of evolution of stars depends on the mass of the star: The greater the mass of the star, the faster this evolution, and the more quickly it leaves the main-sequence, entering either a subgiant or giant phase. In the case of Algol and other binary stars we can observe something completely different: The less massive star is already a subgiant, and the star with much greater mass is still on the main-sequence. Initially, this seems paradoxical as the partner stars of the binary are thought to have formed at approximately the same time and so should have similar ages. Thus the more massive star, rather than the less massive one, should have left the main sequence. The paradox is resolved by the fact that in many binary stars, there can be a flow of material between the two stars, disturbing the normal process of stellar evolution. As the flow progresses, the evolutionary stage of the stars will advance, even as the relative masses change. Eventually, the originally more massive star will reach the next stage in its evolution despite having lost much of its mass to its companion.
Alike and Unlike
Release Date: //-460
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: If things are many... they must be both like and unlike. But that is impossible; unlike things cannot be like, nor like things unlike. Authored by Zeno.
Description: According to Plato in Parmenides 127-9, Zeno argued that the assumption of plurality_the assumption that there are many things_leads to a contradiction. He quotes Zeno as saying: "If things are many, . . . they must be both like and unlike. But that is impossible; unlike things cannot be like, nor like things unlike" (Hamilton and Cairns (1961), 922). Zeno's point is this. Consider a plurality of things, such as some people and some mountains. These things have in common the property of being heavy. But if they all have this property in common, then they really are all the same kind of thing, and so are not a plurality. They are a one. By this reasoning, Zeno believes it has been shown that the plurality is one (or the many is not many), which is a contradiction. Therefore, by reductio ad absurdum, there is no plurality, as Parmenides has always claimed. Plato immediately accuses Zeno of equivocating. A thing can be alike some other thing in one respect while being not alike it in a different respect. Your having a property in common with some other thing does not make you identical with that other thing. Consider again our plurality of people and mountains. People and mountains are all alike in being heavy, but are unlike in intelligence. And they are unlike in being mountains; the mountains are mountains, but the people are not. As Plato says, when Zeno tries to conclude "that the same thing is many and one, we shall [instead] say that what he is proving is that something is many and one [in different respects], not that unity is many or that plurality is one...." [129d] So, there is no contradiction, and the paradox is solved by Plato. This paradox is generally considered to be one of Zeno's weakest paradoxes, and it is now rarely discussed. [See Rescher (2001), pp. 94-6 for some discussion.]
Allais Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: A change in a possible outcome that is shared by different alternatives affects people's choices among those alternatives, in contradiction with expected utility theory. Authored by Maurice F lix Charles Allais.
Description: The Allais paradox arises when comparing participants' choices in two different experiments, each of which consists of a choice between two gambles, A and B.
Antitrust Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Legal intervention artificially raised prices by protecting inefficient competitors from competition. Authored by Robert Bork.
Description: The Antitrust Paradox is a 1978 book by Robert Bork that criticized the state of United States antitrust law in the 1970s. A second edition, updated to reflect substantial changes in the law, was published in 1993. It is claimed that the work is the most cited book on antitrust. Bork has credited Aaron Director as well as other economists from the University of Chicago as influences.
Apportionment Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: The rules for apportionment in a political system can produce results which are unexpected or seem to violate common sense.
Description: An apportionment paradox exists when the rules for apportionment in a political system produce results which are unexpected or seem to violate common sense. To apportion is to divide into parts according to some rule, the rule typically being one of proportion. Certain quantities, like milk, can be divided in any proportion whatsoever; others, such as horses, cannot - only whole numbers will do. In the latter case, there is an inherent tension between our desire to obey the rule of proportion as closely as possible and the constraint restricting the size of each portion to discrete values. This results, at times, in unintuitive observations, or paradoxes. Several paradoxes related to apportionment, also called fair division, have been identified. In some cases, simple adjustments to an apportionment methodology can resolve observed paradoxes. Others, such as those relating to the United States House of Representatives, call into question notions that mathematics alone can provide a single, fair resolution. Some systems of apportioning representation can have unintuitive results due to rounding
Archer's Paradox
Release Date: //1913
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: An archer must, in order to hit his target, not aim directly at it, but slightly to the side. Authored by E.J. Rendtroff.
Description: The term archer's paradox refers to the phenomenon of an arrow traveling in the direction it is pointed at at full draw, when it seems that the arrow would need to pass through the starting position it was in before being drawn, where it was pointed to the side of the target. The bending of the arrow (around the bow), when released, is the explanation of the paradox and should not be confused with the paradox itself. Flexing of the arrow when shot from a modern 'center shot' bow is still present and is caused by a variety of factors, mainly the way the string is deflected from the fingers as the arrow is loosed. The term was first used by E.J. Rendtroff in 1913, and as understanding was gained about the arrow flexing out of the way of the bow as it is shot (as first filmed by Clarence Hickman) and then experiencing oscillating back-and-forth bending as it travels toward the target,[4] this dynamic flexing has incorrectly become a common usage of the term, causing misunderstanding by those only familiar with modern target bows, which being 'centre shot' do not actually show any paradoxical behaviour as the arrow is always pointing visually along its line of flight.
Archimedes Paradox (aka the Hydrostatic Paradox)
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: A massive battleship can float in a few litres of water. Authored by Archimedes.
Description: The Archimedes paradox, named after Archimedes of Syracuse, or the hydrostatic paradox, states that an object can float in a quantity of water that has less volume than the object itself, if its average density is less than that of water. A more general formulation of the paradox is that "that any quantity of water, or other fluid, how small whatsoever, may be made to balance and support any quantity, or any weight, how great whatsoever". The implication of this is that a large, massive object can float in a relatively small volume of liquid, provided that it is surrounded by it. One extreme application of the paradox is that a battleship can float in a few buckets of water, provided that the water surrounds the hull completely and that the ship would have floated had it been in open water.
Aristotle's Wheel Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Rolling joined concentric wheels seem to trace the same distance with their circumferences, even though the circumferences are different. Authored by Aristotle.
Description: Aristotle's wheel paradox is a paradox from the Greek work Mechanica traditionally attributed to Aristotle. There are two wheels, one within the other, whose rims take the shape of two circles with different diameters. The wheels roll without slipping for a full revolution. The paths traced by the bottoms of the wheels are straight lines, which are apparently the wheels' circumferences. But the two lines have the same length, so the wheels must have the same circumference, contradicting the assumption that they have different sizes: a paradox. The fallacy is the assumption that the smaller wheel indeed traces out its circumference, without ensuring that it, too, rolls without slipping on a fixed surface. In fact, it is impossible for both wheels to perform such motion. Physically, if two joined concentric wheels with different radii were rolled along parallel lines then at least one would slip; if a system of cogs were used to prevent slippage then the wheels would jam. A modern approximation of such an experiment is often performed by car drivers who park too close to a curb. The car's outer tire rolls without slipping on the road surface while the inner hubcap both rolls and slips across the curb; the slipping is evidenced by a screeching noise. Alternatively, the fallacy is the assumption that the smaller wheel is independent of the larger wheel. Imagine a tire as the larger wheel, and imagine the smaller wheel as the interior circumference of the tire and not as the rim. The movement of the inner circle is dependent on the larger circle. Thus its movement from any point to another can be calculated by using an inverse of their ratio.
Arrow Information Paradox
Release Date: //1962
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: To sell information you need to give it away before the sale. Authored by Kenneth Arrow.
Description: The Arrow information paradox, named after Kenneth Arrow, American economist and joint winner of the Nobel Memorial Prize in Economics with John Hicks, is a problem that companies face when managing intellectual property across their boundaries. This happens when they seek external technologies for their business or external markets for their own technologies. It has implications for the value of technology and innovations as well as their development by more than one firm and for the need for and limitations of patent protection. Arrow's information paradox theory was set out in a 1962 paper. Cornell Law School professor Oskar Litvak has written in a paper for a conference at Stanford University that Arrow's "paper has been one of the foundational theoretical pillars of the incentive based theory of patents as Arrow's work is thought to rule out a strictly market based solution." A fundamental tenet of the paradox is that the customer, i.e. the potential purchaser of the information describing a technology (or other information having some value, such as facts), wants to know the technology and what it does in sufficient detail as to understand its capabilities or have information about the facts or products to decide whether or not to buy it. Once the customer has this detailed knowledge, however, the seller has in effect transferred the technology to the customer without any compensation. This has been argued to show the need for patent protection. If the buyer trusts the seller, or is protected via contract, then they only need to know the results that the technology will provide, along with any caveats for its usage in a given context. A problem is that sellers lie, they may be mistaken, one or both sides overlook side consequences for usage in a given context, or some unknown unknown affects the actual outcome. Discussions of the value of patent rights have taken Arrow's information paradox into account in their evaluations. The theory has been the basis for many later economic studies. These include theories that pre-patent innovation can be carried out only by a single firm.
Arrow Paradox
Release Date: //-460
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: If everything when it occupies an equal space is at rest, and if that which is in locomotion is always occupying such a space at any moment, the flying arrow is therefore motionless. Authored by Zeno.
Description: Zeno's Arrow Paradox takes a different approach to challenging the coherence of our common sense concepts of time and motion. As Aristotle explains, from Zeno's ñassumption that time is composed of moments,î a moving arrow must occupy a space equal to itself during any moment. That is, during any moment it is at the place where it is. But places do not move. So, if in each moment, the arrow is occupying a space equal to itself, then the arrow is not moving in that moment because it has no time in which to move; it is simply there at the place. The same holds for any other moment during the so-called ñflightî of the arrow. So, the arrow is never moving. Similarly, nothing else moves. The source for Zeno's argument is Aristotle (Physics, Book VI, chapter 5, 239b5-32). In the arrow paradox (also known as the fletcher's paradox), Zeno states that for motion to occur, an object must change the position which it occupies. He gives an example of an arrow in flight. He states that in any one (duration-less) instant of time, the arrow is neither moving to where it is, nor to where it is not.[13] It cannot move to where it is not, because no time elapses for it to move there; it cannot move to where it is, because it is already there. In other words, at every instant of time there is no motion occurring. If everything is motionless at every instant, and time is entirely composed of instants, then motion is impossible. Whereas the first two paradoxes divide space, this paradox starts by dividing timeand not into segments, but into points. If everything when it occupies an equal space is at rest, and if that which is in locomotion is always occupying such a space at any moment, the flying arrow is therefore motionless. _ as recounted by Aristotle, Physics VI:9, 239b5
Arrow's Impossibility theorem
Release Date: //1951
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Given more than two choices, no system can have all the attributes of an ideal voting system at once. Authored by Kenneth Arrow.
Description: In social choice theory, Arrow's impossibility theorem, the General Possibility Theorem, or Arrow's paradox, states that, when voters have three or more distinct alternatives (options), no rank order voting system can convert the ranked preferences of individuals into a community-wide (complete and transitive) ranking while also meeting a pre-specified set of criteria. These pre-specified criteria are called unrestricted domain, non-dictatorship, Pareto efficiency, and independence of irrelevant alternatives. The theorem is often cited in discussions of election theory as it is further interpreted by the Gibbard-Satterthwaite theorem.
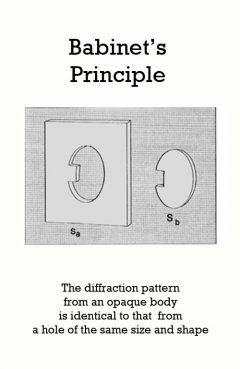
Babinet's principle Babinet's paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: The diffraction pattern from an opaque body is identical to that from a hole of the same size and shape. Authored by Jacques Babinet.
Description: In physics, Babinet's principle is a theorem concerning diffraction that states that the diffraction pattern from an opaque body is identical to that from a hole of the same size and shape except for the overall forward beam intensity.
Bald Man Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: A man with a full head of hair is not bald. The removal of a single hair will not turn a non-bald man into a bald one. And yet it is obvious that a continuation of that process must eventually result in baldness.
Description: A man with a full head of hair is obviously not bald. Now the removal of a single hair will not turn a non-bald man into a bald one. And yet it is obvious that a continuation of that process must eventually result in baldness.
The Banach-Tarski Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: Cut a ball into 5 pieces, re-assemble the pieces to get two balls, both of equal size to the first. The von Neumann paradox is a two-dimensional analogue. Authored by Stefan Banach and Alfred Tarski.
Description: he Banach-Tarski paradox is a theorem in set-theoretic geometry which states the following: Given a solid ball in 3 dimensional space, there exists a decomposition of the ball into a finite number of non-overlapping pieces (i.e., disjoint subsets), which can then be put back together in a different way to yield two identical copies of the original ball. The reassembly process involves only moving the pieces around and rotating them, without changing their shape. However, the pieces themselves are not "solids" in the usual sense, but infinite scatterings of points. A stronger form of the theorem implies that given any two "reasonable" solid objects (such as a small ball and a huge ball), either one can be reassembled into the other. This is often stated colloquially as "a pea can be chopped up and reassembled into the Sun." The reason the Banach-Tarski theorem is called a paradox is that it contradicts basic geometric intuition. "Doubling the ball" by dividing it into parts and moving them around by rotations and translations, without any stretching, bending, or adding new points, seems to be impossible, since all these operations preserve the volume, but the volume is doubled in the end.
The Barber Paradox
Release Date: //
Country of Release:
Length:
MPAA:
Medium: Paradox
Genre:
Release Message: A barber (who is a man) shaves all and only those men who do not shave themselves. Does he shave himself? Authored by Bertrand Russell.
Description: The barber paradox is a puzzle derived from Russell's paradox. It was used by Bertrand Russell himself as an illustration of the paradox, though he attributes it to an unnamed person who suggested it to him. It shows that an apparently plausible scenario is logically impossible. Specifically, it describes a barber who is defined such that he both shaves himself and does not shave himself. (Russell's popularization of his set theoretic paradox.) OR An adult male barber shaves all men who do not shave themselves, and no one else. Can he shave himself? Flaws in accepted reasoning