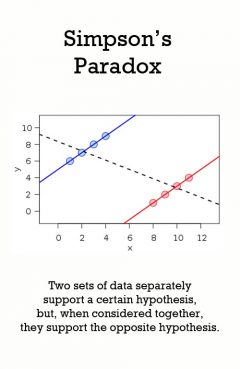
Release Message:  An association in sub-populations may be reversed in the population. Authored by Edward H. Simpson.

Description:  In probability and statistics, Simpson's paradox, or the Yule-Simpson effect, is a paradox in which a trend that appears in different groups of data disappears when these groups are combined, and the reverse trend appears for the aggregate data. This result is often encountered in social-science and medical-science statistics,[1] and is particularly confounding when frequency data are unduly given causal interpretations.[2] Simpson's Paradox disappears when causal relations are brought into consideration. Though it is mostly unknown to laypeople, Simpson's paradox is well known to statisticians, and it is described in a few introductory statistics books.[3][4] Many statisticians believe that the mainstream public should be informed of the counter-intuitive results in statistics such as Simpson's paradox.[5][6] Edward H. Simpson first described this phenomenon in a technical paper in 1951,[7] but the statisticians Karl Pearson, et al., in 1899,[8] and Udny Yule, in 1903, had mentioned similar effects earlier.[9] The name Simpson's paradox was introduced by Colin R. Blyth in 1972.[10] Since Edward Simpson did not actually discover this statistical paradox (an instance of Stigler's law of eponymy), some writers, instead, have used the impersonal names reversal paradox and amalgamation paradox in referring to what is now called Simpson's Paradox and the Yule-Simpson effect.[11]